Hallo Christina,
um dies zu realisieren benötigst Du noch eine Angabe in welche Richtung (in 3D) auf der Ebene das \(x\) aus der 2D-Welt zeigen soll. Daher eignet sich in diesem Fall besser die Parameterdarstellung zur Darstellung der Ebene. Das \(\vec{u}\) gibt die Richtung von \(x\) vor:
$$E: \space \vec{x} = \vec{l} + \vec{u} \cdot s + \vec{v} \cdot t $$ mit:\( \quad \vec{u}, \vec{v} \perp \vec{n}, \quad |\vec{u}|=|\vec{v}| = 1\) wenn Du keine Skalierung wünschst und \(\vec{u} \perp \vec{v}\). Daraus bildest Du eine Matrix \(A\) mit der man die 3D-Koordinaten berechnen kann:
$$\vec{r}_{3D} = A \cdot \vec{r} + \vec{l} = \begin{pmatrix} \vec{u} & \vec{v} \end{pmatrix} \cdot \vec{r} + \vec{l} $$
Beispiel: \(\vec{r}\) sei die Kontour eines Dreiecks mit den Eckpunkten
$$\vec{r} = \left\{ \begin{pmatrix} 0 \\ 0 \end{pmatrix}, \begin{pmatrix} 3 \\ 0 \end{pmatrix}, \begin{pmatrix} 0 \\ 2 \end{pmatrix} \right\}$$
und die Ebene ist definiert durch \(\vec{n} = \begin{pmatrix} 0 & 0,6 & 0,8\end{pmatrix}^T \) und \(\vec{l} = \begin{pmatrix} 1 & 2 & 3\end{pmatrix}^T\) und ich wähle noch ein \(\vec{u} = \begin{pmatrix} 0,5528 & -0,6667 & 0,5 \end{pmatrix}^T\). Daraus ergibt sich dann \(\vec{v} = \vec{n} \times \vec{u}\) und die Matrix A:
$$A = \begin{pmatrix} \vec{u} & \vec{v} \end{pmatrix} = \begin{pmatrix} 0,5528 & 0,8333 \\ -0,6667 & 0,4422\\ 0,5 & -0,3317 \end{pmatrix}$$ rechnet man nun mit Hilfe des Terms für \(r_{3D}\) die drei Eckpunkte des Dreiecks in 3D um, dann erhält man folgendes Bild:
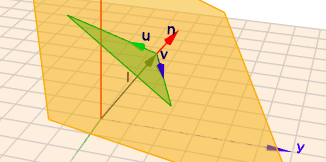
(klick auf das Bild und rotiere die Szene mit der Maus)