1. Bestimme rechnerisch die Geradengleichung der Geradeng, die durch die Beiden Punkte P(5/1) und Q (-2/4,5) verläuft.
Am einfachsten ist die Punkt-Steigungs-Form.
f(x) = (1 - 4,5)/(5 - (-2))*(x - 5) + 1
Man braucht das nicht mal vereinfachen wenn es nicht gefordert ist.
f(x) = -1/2*(x - 5) + 1 = -0,5x + 3,5
2.Gegeben ist die Funktion f mit f(x)= 1/2 x^2 - 3/2
a ) gib die definitionsmenge und die wertemenge von f an
D = R
W = [-3/2 ; ∞]
b)Zeichne das Schaubild Gf der Funktion f für x E ( -4;4)in ein Koordinatensystem ein
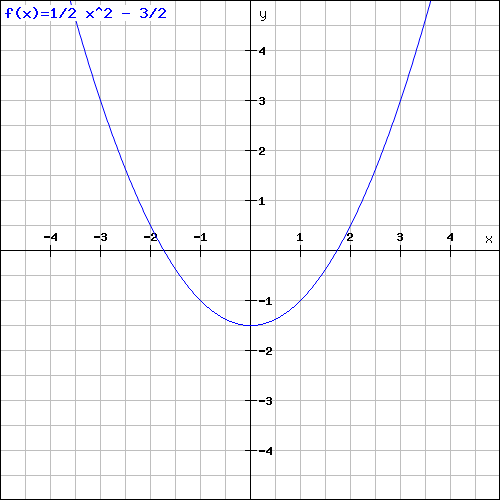
c) berechne alle Schnittpunkte von Gf mit der x-Achse
f(x) = 0
1/2 x^2 - 3/2 = 0
x = +- Wurzel(3)
3. Berechne ausführlich(d.hOhne Ableitungsregeln zu verwenden) die Ableitung der Funktion f mit f(x)= x^2 + x an der Stelle x0= -1
f(x + h) - f(x) / h
= ((x + h)^2 + (x + h) - x^2 - x) / h
= (x^2 + 2h + h^2 + x + h - x^2 - x) / h
= (2xh + h^2 + h) / h
= (2x + h + 1) für h -> 0 ist der Term
= 2x + 1
= 2*-1 + 1 = -1
4. Gib jeweils die Ableitungsfunktion f´der funktion f an:
a) f(x)= 2x^4 - 5x^2 + x - 5,5
f'(x) = 8x^3 - 10x + 1
b) f(x)=1/3 x^-3 - 3/2 x^-2 - x^-1
f'(x) = -x^-4 + 3x^-3 + x^-2
c) f(t) = x^5 + 5t
f'(t) = 5
5.wie verändert sich der Graph Gf der Ableitungsfunktion f wenn der Graph Gf der Funktion f
a ) nach unten verschoben wird
gar nicht
b) nach oben verschoben wird
gar nicht
6. gibt es eine stelle x_{0}, an der die drei Funktionen f mit
f(x)=x hoch 2+ 3, g mit
f'(x) = 2x
g(x)=2/3 x hoch 3 sowie h mit
g'(x) = 2x^2
h(x)=2x + 6 die gleiche Ableitung haben ?
h'(x) = 2
An der Stelle x_{0} = 1 haben alle die Steigung 2.