Dreieck drehen und spiegeln

Question

Himfee Hallo. Was für eine Überlegung muss ich hier feststellen?

Dreieck drehen und spiegeln
Zeichnen Sie ein gleichseitiges Dreieck (mit Seitenlängen 4cm) und beschriften Sie die Eckpunkte entgegen dem Uhrzeigersinn mit A, B und C.
a) Führen Sie mit diesem Dreieck die Drehung DC, 120° durch.
b) Führen Sie am ursprünglichen Dreieck ABC nacheinander die Geradenspiegelungen
SCA und SCB aus. Was fällt Ihnen auf?

Answer 1

Wenn man das gleichseitiges Dreieck $\triangle ABC$ (braun) um 120° (blauer Winkel) um den Punkt $C$ dreht, so kommt man  zum grünen Dreieck $\triangle A^*B^*C$:

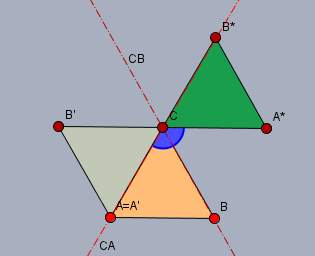
Spiegelt man das gleiche Ausgangsdreieck $\triangle ABC$ an der Geraden durch $CA$ kommt man nach $\triangle ACB'$ und anschließend nach einer Spiegelung an der Geraden durch $CB$ wieder zum grünen Dreieck $\triangle A^*B^*C$.

Was für eine Überlegung muss ich hier feststellen?

Beide Abbildungen haben den gleichen Effekt.

Allgemein gilt: zwei Spiegelungen sind identisch zu einer Rotation um den doppelten Winkel in dem die Spiegelachsen zu einander stehen.

Gruß Werner

Answer 2

Hm,

ich hab die Anweisungen, so wie ich sie verstanden hab ausgeführt.

Drehung ABC um C,120°
Siegelung ABC an Gerade(A,C) ===> ABC_1

Siegelung ABC_1 an Gerade(B,C) ===> A'_2BC

War das so zu verstehen und wo sind Deine Probleme?