Hallo eliboy,
wenn Du Dir nicht nur ein Schrägbild zeichnest, sondern die Punkte und ggf. Flächen und Strecken auch hier im Geoknecht3D eingibst, so bekommst Du ein gutes Bild der Szene und kannst auch Deine Rechenergebnisse kontrollieren.
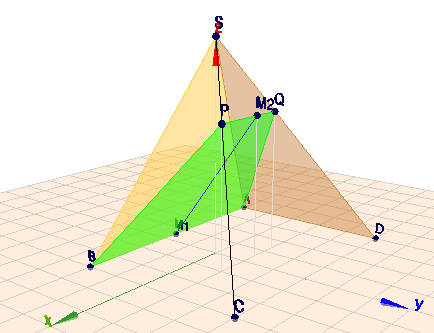
(klick auf das Bild und drehe die Szene mit der Maus)
Dort siehst Du auch, dass \(M_2\) auf der Strecke \(PQ\) liegt.
Weisen Sie nach, dass \(M_1M_2\) orthogonal zu \(AB\) liegt.
Du weißt sicher, dass das Skalarprodukt zweier Vektoren, zu 0 wird, wenn diese senkrecht (bzw. orthogonal) auf einander stehen. Das kann man hier nachprüfen:
$$\vec{AB} \cdot \vec{M_1M_2} \\ \space = (B-A) \cdot (M_2 - M_1)\\ \space = \left( \begin{pmatrix} 3 \\ -2 \\ 0\end{pmatrix} - \begin{pmatrix} -4 \\ -2 \\ 0\end{pmatrix} \right) \cdot \left( \begin{pmatrix} -0,5\\ 1 \\ 4\end{pmatrix} - \begin{pmatrix} -0,5 \\ -2 \\ 0\end{pmatrix} \right) \\ \space = \begin{pmatrix} 7 \\ 0 \\ 0\end{pmatrix} \cdot \begin{pmatrix} 0 \\ 3 \\ 4 \end{pmatrix} \\ \space = 7\cdot 0 + 0 \cdot 3 + 0 \cdot 4 = 0$$
Wenn diese Vektoren bzw. Strecken senkrecht zueinander stehen, dann ist \(|M_1M_2|\) auch die Höhe im Trapez \(ABPQ\). Dann kannst Du die bekannte Flächenformel für das Trapez verwenden. Die einzelnen Strecken und die Fläche sind:
$$\begin{aligned} a &= |AB| = 7 \\ c &= |PQ| = 1 - (-\frac43) =\frac73 \\ h &= |M_1M_2| = \sqrt{0^2+3^2+4^2} = 5 \\ F_T &= \frac12 (a+c) h = \frac12 (7 + \frac{7}{3}) 5 = \frac{70}3 \approx 23,3 \end{aligned}$$