Aufgabe 4. Sei A = (nij ) eine m × n-Matrix mit ganzzahligen Einträgen,
aufgefasst als Element A ∈ Matm×n(Q). Für jedes Primzahl p > 0 sei
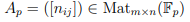
die Matrix, deren Einträge die Kongruenzklassen von nij ∈ Z modulo p sind.
Beweisen Sie mithilfe des Gauß-Algorithmus, dass
rank(A) = rank(Ap)
für fast alle Primzahlen p > 0.