Formel bzw. Algorithmus aus Matrix ableiten

Question

Hallo liebe mathelounge Community,

ich habe folgendes Problem.

Aufgabe:

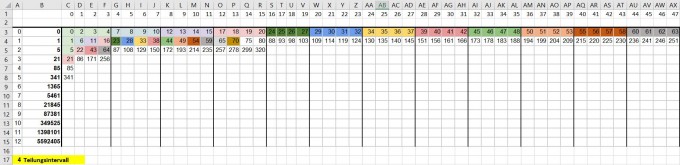
es soll aus einer Matrix (siehe Bild) eine Formel bzw. folgend daraus ein Algorithmus abgeleitet werdem, mit dem sich jeder beliebige Wert der Matrix bestimmen lässt.

Konstante: Intervall i=4 (theoretisch funktioniert es mit jedem beliebigen Intervall von 2 bis 128)

Es gibt einen Baum, dessen Knoten in folgender Reihenfolge besucht werden sollen:

Für jeden Knoten, muss die Schrittnummer ermittelt werden können. Umgekehrt muss aus der Schrittnummer, die Position im Baum ermittel werden können.

Die Matrix ist folgendermaßen aufgebaut:
In der ersten Zeile 0 wird von 0 in ganzen Zahlen aufwärts gezählt, wobei nach jedem Intervall (4 Spalten) die nächst höhere ganze Zahl in nächste Zeile geschrieben wird.
Zu Beginn, benötige ich die 1 in Zeile 1 Spalte 0, um das erste Intervall der Zeile 0 "vervollständigen" zu können.
Immer, wenn ein Intervall in Zeile 0 "voll" ist, wird die nächst höhere Zahl in die darunterliegende Zeile ganz links geschrieben, bevor das nächste Intervall in Zeile 0 fortgesetzt wird.
Ist das Intervall der darunterliegenden Zeile "voll", wird die nächst höhere Zahl wiederum in die darunterliegende Zeile geschrieben, danach die nächst höhere Zahl in die darüberliebende Zeile, bevor ein ganzes Intervall in Zeile 0 geschrieben wird. Dies wiederholt sich, bis man wieder in Zeile 0 weiterzählen kann.

Problem/Ansatz:

Es ist mir bereits gelungen, die Formel für die Spalte 0 aufzustellen. Die Formel soll jedoch letztendlich alle Werte der Matrix auslesen können und muss daher auch die x Komponente (horizontal) enthalten und daher w[i](x,y)=... lauten.

Hier ist die Formel für Spalte 0:

\( w[i](0,y)=\frac{i^y-1}{i-1} \)

Das Intervall i beträgt in diesem Beispiel wie bereits erwähnt 4. Wenn ich nun in der obigen Formel für die Zeilennummer y die entsprechenden Werte eintage, komme ich genau auf die Werte der Spalte 0 der Matrix. Die Formel ist in Spalte B der Matrix in der Excel Datei bereits eingesetzt.

Mir gelingt es jedoch nicht, die horizontale Dimension x einzubauen, sodass ich jeden beliebigen Wert berechnen kann.

Es wäre mir sehr geholfen, wenn jemand die Lösung zu diesem Problem findet.

!

LG
feige73e

Hier ist ein Bild der Matrix:

Answer 1

Erstmal vorne weg. Ich finde es extrem unfair die Frage über, inzwischen mind. 4 Matheforen zu verteilen ohne die Prozessbeteiligten zu informieren, sie parallel und aneinander vorbei arbeiten zu lassen: -(

Ich bezweifle auch, dass die Reihe in eine XL-Formel gezwängt werden kann. Du hast eine Liste an Ausnahmen(Deine Werte in Spalte 0 und die mod i aussortierten), die im allgemeinen Fall geprüft werden muss bevor die nächste Position in der Reihe besetzt werden kann. Für variable i ist das formeltechnisch nicht zu machen (behaupte ich jetzt mal). Die Buchführung wäre eventuell per Makro zu handeln...

Nachtrag:

Adenauer: "Was interessiert mich mein dummes Geschwätz von gestern."
Also es geht doch, weil der Tabellenaufbau, so wie es aussieht, abweichend von der Prozessbeschreibung modulo Spaltennummer und Intervalpotenz berechnet werden kann. Beispiel unten im Kommentar...

Comments

Gut, schaun wir weiter...

Ist sicher, dass die Spalte 0 so aussehen muss, wie sie aussieht.

Wie auf dem Matheplanet festgestellt spielt sie ein Sonderrolle.
Kaum hast Du Deinen Zählreim aufgesagt (>von 0 in ganzen Zahlen aufwärts gezählt), revidierst Du Dich, um plötzlich die Spalte 0 vorzubelegen.

>wenn ein Intervall in Zeile 0 "voll" ist, wird die nächst höhere Zahl in die darunterliegende Zeile ganz links geschrieben

Ja, von wegen, schon im ersten Intervall wird die 5 zwei Zeilen runtergesetzt, auch bei Intervallgrenze 20..24. Es sieht so aus als ob an den Intervallgrenzen Modulo i^zi (Interval i, zi Zeilen 1..12) auch entsprechend viele Zeilen aufgefüllt werden?

Als Beispiel der letzte Tabellenwert 340, der seine Folgewerte auf die Zeile 5..0 verteilt - ist das so richtig?

Hast Du Beispiele für andere Intervalle 2,3,5,6 oder so...

---

Ich habe einen Ansatz für die Lösung gefunden, und zwar hat der Baum den ich konstruiere sogar einen Namen, er wird nach der Regel "depth-first in-order enumeration" gebildet.

https://math.stackexchange.com/questions/1670012/determine-depth-of-node-in-perfect-binary-tree-with-depth-first-in-order-enumera

https://stackoverflow.com/questions/30013591/binary-tree-find-position-in-inorder-traversal

Ich denke, die einzelnen Zellen lassen sich per Formel nicht definieren, sondern nur rekursiv.

Falls jemand dennoch eine Formel findet, lasst es mich bitte wissen :)

---

Wenn, der Aufbau so laufen soll, wie oben dargestellt, dann hab ich vermutlich eine Lösung, die eventuell sogar variable Intervalle aushält. Sind ein paar Array-Formeln notwendig, weil ich mich mehr am Tabellenaufbau orientiert hab und die mathematischen Betrachtungen etwas aus den Augen verloren habe.

Allerdings stößt die Tabelle an der Spaltengrenze an. Sinnvoller wäre ein transponierter Aufbau gewesen?

Hast Du eine Antwort auf meine Fragen oben? Kürzere Antwortintervalle wären angebracht - ich muss mich nach Tagen immer wieder neu reindenken - fasst hätt ich die XL-Tabelle entsorgt...

Auf dem vor Dir angesprochenen Weg (rekursiv oder iterativ) war ich zuerst auch, deshalb der Hinweis das mit Makro zu machen - ich glaub zuviel Mathemaitk behindert die TabKalk-Denke ;-)...

---

Danke erstmal für deine Mühen wächter und sorry für die verzögerte Antwort!

Ja, ich habe eine Antwort auf deine obige Frage:

>Ja, von wegen, schon im ersten Intervall wird die 5 zwei Zeilen runtergesetzt, auch bei Intervallgrenze 20..24. Es sieht so aus als ob an den Intervallgrenzen Modulo izi (Interval i, zi Zeilen 1..12) auch entsprechend viele Zeilen aufgefüllt werden?<

Die 5 in der Spalte 0 kommt daher zu Stande, weil immer, wenn das Intervall der darüberliegenden Zeile "voll" ist, die nächsthöhere Zahl in eine neue Spalte geschrieben werden muss. Das ist eine Bedingung. Und da das Intervall der Zeile 0 mit der Zahl 4 "voll" ist, und in Zeile 1 bereits eine Zahl steht, muss die 5 in Zeile 2.

Selbiges gilt für Intervallgrenze 20.

In welche Richtung geht deine Lösung?

---

Meine Formeln:

Namen
ZNR=Tabelle1!$A$7:$A$18
Spalte0=Tabelle1!$C$6:$C$18
Zeile0=Tabelle1!$C$6:$NB$6

Spalte D ( kopierfertig über alle SpaltenZeilen)

D6:{=SUMME(C6;1;1*(REST(SPALTE()-3;i^(ZNR))=0);1*((C6+1)=Spalte0))}
 D7:=INDEX(Zeile0;(SPALTE()-3)*i+1)-(ZEILE()-6)
 D8:=INDEX(Zeile0;(SPALTE()-3)*i^(ZEILE()-6)+1)-(ZEILE()-6)
 D9:=INDEX(Zeile0;(SPALTE()-3)*i^(ZEILE()-6)+1)-(ZEILE()-6)
D10:=INDEX(Zeile0;(SPALTE()-3)*i^(ZEILE()-6)+1)-(ZEILE()-6)
D11:=INDEX(Zeile0;(SPALTE()-3)*i^(ZEILE()-6)+1)-(ZEILE()-6)

Knoten by Zeilen/Spalten-Index
Index Zeile Spalte "Wert des Knoten" "Zeile0 Spalte"
 0 idx0 {=SUMME(idx0+1;GANZZAHL(idx0/i^ZNR);GANZZAHL(LOG(idx0;i)))} 
 idy idx {=SUMME(idxy0;GANZZAHL(idxy0/i^ZNR);GANZZAHL(LOG(idxy0;i)))-idy} idxy0=idx*i^idy+1