Stetige Zufallsvariablen. Begründen, dass G(x) eine Verteilungsfunktion ist.

Question

Aufgabe:

es wird die folgende Funktion betrachtet
G(x)=
0 für x<−2
1/3für x∈[−2,−1/2)
23 für x∈[−1/2,1)
1 für x ≥ 1
Begründen Sie, dass G(x) eine Verteilungsfunktion ist. Geben Sie explizit das zugehörige
Wahrscheinlichkeitsmaß an.

Problem/Ansatz:

Für alle, die mir helfen möchten
ich bräuchte bitte einen kompletten Lösungsweg

Comments

Du meintest vermutlich:

G(x)=
0 für x<−2
1/3für x∈[−2,−1/2)
2/3 für x∈[−1/2,1)
1 für x ≥ 1

Oder?

Answer 1

Hallo Anna, zeichne bitte mal im ersten Schritt die Funktion G(x). 

Comments

Ich habe das bezeichnet  und danach was soll ich machen?

---

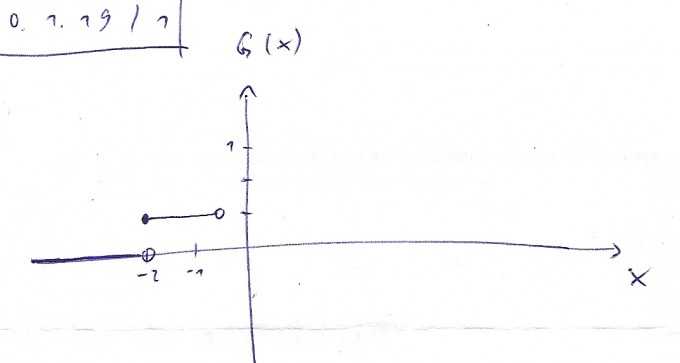
Hallo Anna, das ist leider falsch.  Nach rechts wird x aufgetragen, und nach oben G(x).  Wenn z. B. x = -3, dann ist G(x) = 0.  Und wenn x = -1, dann ist G(x) = 1/3.  Hier habe ich den Anfang gemacht.  Wie geht es weiter?  Bitte beachte noch, dass in deiner Aufgabe „23“ steht, was falsch ist.  Korrekt ist „2/3“.

---

Danke Schön ,dann jetzt ich muss zwei denge begründen :zu erst das G(x)>0 und danach das G(X) =1 ist das richtig ?

---

Hallo Anna, bitte zeichne zunächst G(x).

---

Ist das Richtig so?

---

Genau.  Da G(x) angibt, wie groß die Wahrscheinlichkeit für x oder kleiner ist, muss G(x) monoton steigen, also von links nach rechts immer größer werden.  Außerdem muss G(x) ganz links 0 und ganz rechts 1 sein.  Dann ist G(x) eine Verteilungsfunktion.  Ist das hier der Fall?

---

Na klar es ist so

Ich muss noch die erste teile genau 0 machen ,Danke Schön

Aber es gibt noch die Warscheinlischkeismaß wie kann ich die bearbeiten

---

In dem beigefügten Bild siehst du das Wahrscheinlichkeitsmaß.  Es gibt verschiedenen Darstellungen, ich habe eine davon gewählt.  Mathematisch nicht ganz exakt.  Daraus kannst du ablesen:  Die Wahrscheinlichkeit, dass x = -2 ist, ist 1/3.  Und so weiter.

---

das war sehr hilfreich, danke sehr

---

Vielen Dank für "beste Antwort", und jederzeit gerne wieder.