Fragen zur achsensymmetrie spiegeln

Question

Aufgabe: Achsensymmetrie

zeichne in ein kordinatensystem mit einheit 1 cm das viereck ABCD mit A(3/2) B(6/5) C(6/9) und D(5/9) mit bleistift in dein heft. Spiegele dann an der Geraden PQ mit P(0/5) und Q(7/5). Wähle für das Spiegelbild eine farbe

Problem/Ansatz:

wie soll ich die Spieglung zeichnen, wenn dass Viereck Vielecken hat

ich habe die Skizze schon vorgezeichnet

Answer 1

Hallo ellatgz,

Führe die Spiegelung für jeden der Punkte einzeln durch. Zeichen dazu eine Gerade, die senkrecht auf der Spiegelgeraden \(PQ\) steht und durch den zu spiegelnden Punkt verläuft. Für den Punkt \(A\) habe ich Dir das mal eingezeichnet:

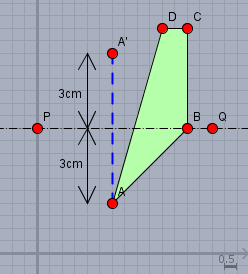
Die blau gestrichelte Gerade steht senkrecht auf \(PQ\) und der gespiegelte Punkt \(A'\) ist von der Geraden genauso weit entfernt, wie der Punkt \(A\) - nämlich \(3\text{cm}\) bzw. 6 Kästchen auf dem Papier. Der Punkt \(B\) liegt auf der Spiegelgeraden \(PQ\) - folglich ist die Entfernung =0 und \(B=B'\); d.h. der Punkt ist auch sein eigenes Spiegelbild. Gehe für die verbleibenden Punkte genauso vor wie für \(A\). Für \(C\) und \(D\) beträgt der Abstand \(4\text{cm}\). Dann erhältst Du

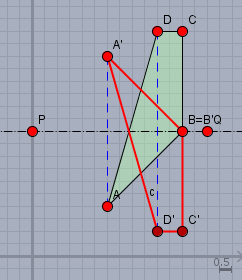
Wenn Du fertig bist, dan nehme einen kleinen Taschenspiegel und stelle ihn senkrecht auf die Gerade \(PQ\). Und dann schaue Dir an, was Du in dem Spiegel siehst.

Gruß Werner

Answer 2

Spiegel jeden einzelnen Punkt an der Geraden und Verbinde dann die gespiegelten Punkte miteinander.