Berechne die Kurvendiskussion zu dieser Funktionsschar fa(x)=a^2 *x*e^{-a*x}.

Question

Gegeben ist die Funktionenschar fa(x)=a²  *x*e^-a*x  . Ihr Graph sei Ga.

1.Bestimmen sie die Koordinaten des Schnittpunktes von Ga mit der x-Achse und geben sie das Verhalten im Unendlichen an. G2 und G4 schneiden sich in den beiden Punkten P und Q . Bestimmen sie die Größe des Winkels, unter dem die Gerade g_PQ die positive x- Achse schneidet.

Answer 1

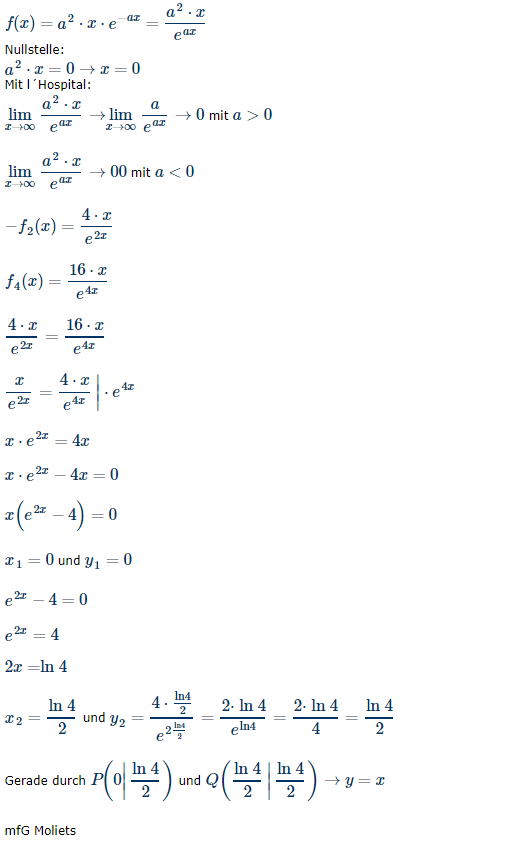
Text erkannt:

\( f(x)=a^{2} \cdot x \cdot e^{-a x}=\frac{a^{2} \cdot x}{e^{a x}} \)
Nullstelle:
\( a^{2} \cdot x=0 \rightarrow x=0 \)
Mit I'Hospital:
\( \lim \limits_{x \rightarrow \infty} \frac{a^{2} \cdot x}{e^{a x}} \rightarrow \lim \limits_{x \rightarrow \infty} \frac{a}{e^{a x}} \rightarrow 0 \) mit \( a>0 \)
\( \lim \limits_{x \rightarrow \infty} \frac{a^{2} \cdot x}{e^{a x}} \rightarrow 00 \) mit \( a<0 \)
\( -f_{2}(x)=\frac{4 \cdot x}{e^{2 x}} \)
\( f_{4}(x)=\frac{16 \cdot x}{e^{4 x}} \)
\( \frac{4 \cdot x}{e^{2 x}}=\frac{16 \cdot x}{e^{4 x}} \)
\( \frac{x}{e^{2 x}}=\frac{4 \cdot x}{e^{4 x}} \mid \cdot e^{4 x} \)
\( x \cdot e^{2 x}=4 x \)
\( x \cdot e^{2 x}-4 x=0 \)
\( x\left(e^{2 x}-4\right)=0 \)
\( x_{1}=0 \) und \( y_{1}=0 \)
\( e^{2 x}-4=0 \)
\( e^{2 x}=4 \)
\( 2 x=\ln 4 \)
\( x_{2}=\frac{\ln 4}{2} \) und \( y_{2}=\frac{4 \cdot \frac{\ln 4}{2}}{e^{2 \frac{\ln }{2}}}=\frac{2 \cdot \ln 4}{e^{\ln 4}}=\frac{2 \cdot \ln 4}{4}=\frac{\ln 4}{2} \)
Gerade durch \( P\left(0 \mid \frac{\ln 4}{2}\right) \) und \( Q\left(\frac{\ln 4}{2} \mid \frac{\ln 4}{2}\right) \rightarrow y=x \)
mfG Moliets

Text erkannt:

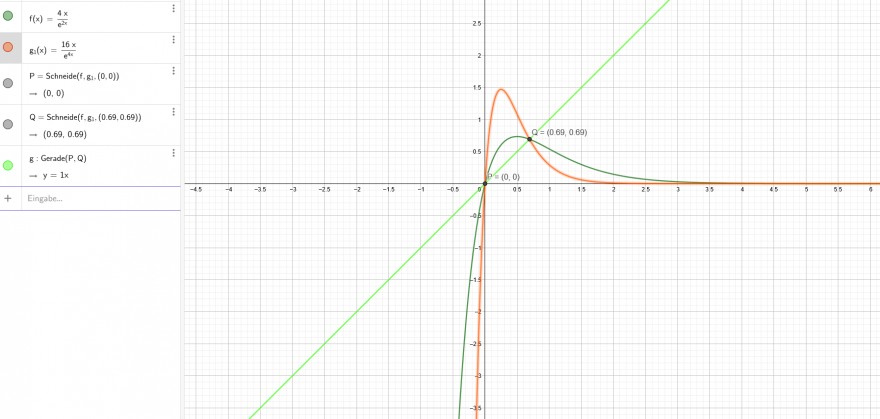
\( f(x)=\frac{4 x}{e^{2 x}} \)
1
B. \( (x)=\frac{16 x}{e^{4}} \)
\( P= \) Schneide \( \left(f, B_{1},(0,0)\right) \)
\( i \)
8
\( -(0,0) \)
\( Q= \) Schocide \( \left(f, g_{1},(0.69,0.69)\right) \)
\( \mathbf{r} \)
1
\( \rightarrow(0.69 .0 .69) \)
: : Gerade(P.Q)
\( i \)
\( -y=2 x \)
+ Eingabe..