Gerade quadratische Pyramide

Question

Aufgabe:

Von einer geraden, quadratischen Pyramide kennt man den Eckpunkt:

A (6,-5,1), die Spitze S (6,1,7)

und die Trägergerade h der Höhe:

X=(6/1/7) + t(2/2/1)

Gesucht sind :

1-)die Koordinaten der Eckpunkte B,C,D

2-)das Volumen der Pyramide

3-)den Winkel zwischen der Basisfläche und einer Seitenkante!

kann jemand mir mit einer ausführlichen Antwort helfen, wie ich von Trägergerade ausgehend eine Höhe und die  Koordinaten ihres Fußpunktes finde?

Vielen Dank!

Answer 1

Der Fußpunkt der Pyramidenhöhe ist (u|v|w)= (6+2k|1+2k|7+k) und das Produkt

[ \( \begin{pmatrix} 6\\-5\\1 \end{pmatrix} \) -\( \begin{pmatrix} u\\v\\w \end{pmatrix} \) ]·\( \begin{pmatrix} 2\\2\\1 \end{pmatrix} \)=0  Damit lässt sich zunächst k bestimmen und dann der Fußpunkt.

Comments

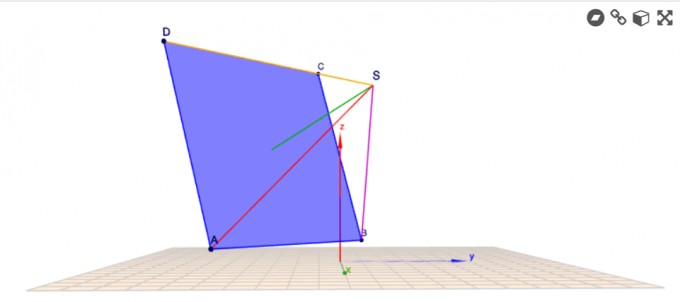
Das sieht so aus

Ebene aufstellen in der die Grundfläche liegt.
E: X·N = A·N
E: X·[2, 2, 1] = [6, -5, 1]·[2, 2, 1]
E: 2·x + 2·y + z = 3

Lotfußpunkt F ermitteln: Gerade h in E einsetzen.
2·(2·r + 6) + 2·(2·r + 1) + (r + 7) = 3 → r = -2
F = [6, 1, 7] - 2·[2, 2, 1] = [2, -3, 5]

Eckpunkt C bestimmen: A an F spiegeln
FA = A - F = [6, -5, 1] - [2, -3, 5] = [4, -2, -4]
C = F - FA = [2, -3, 5] - [4, -2, -4] = [-2, -1, 9]

Richtungsvektor FB bzw. FD bestimmen:
FB = N ⨯ FA = ([2, 2, 1]/|[2, 2, 1]|) ⨯ [4, -2, -4] = [-2, 4, -4]

B = F + FB = [2, -3, 5] + [-2, 4, -4] = [0, 1, 1]
D = F - FB = [2, -3, 5] - [-2, 4, -4] = [4, -7, 9]

Der Rest sollte hoffentlich klar sein. Bei Bedarf frag nochmal nach.

---

Danke schön!