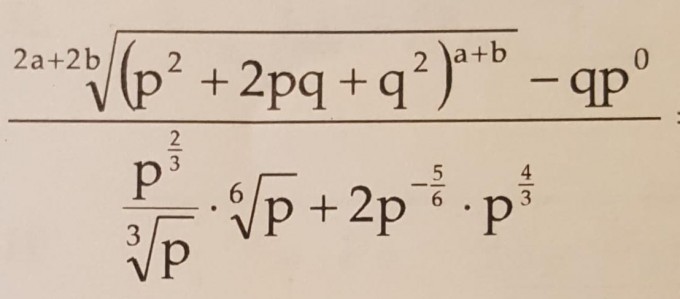Wie löst man diese Potenz/Wurzel Aufgabe?

Question

Aufgabe:

Ich muss so weit wie möglich vereinfachen.

Problem/Ansatz:

Ich schaffe es einfach nicht.

Kann mir bitte jemand zeigen, wie er diese Aufgabe löst. Ich schaffe es immer P zu notieren und P auch richtig zu berechnen, aber bei q und den Zahlen scheitere ich, da ich nicht weiss, wie man mit denen rechnen muss.

Answer 1

p^2+2pq+q^2 ist ne binomische formel, die riesige wurzel kürzt sich fast vollständig weg (wurzel=^(1/2)), etwas^0=1

im Nenner ist es p^(2/3)/p^(1/3)=p^(1/3)     *p^(1/6)=p^(1/2) und 2p...=2p^(1/2) also Nenner= 3p^1/2

Answer 2

Hallo Atorian,$$\frac{\sqrt[2a+2b]{(p^2+2pq+q^2)^{a+b}} - pq^0}{\frac{p^{\frac 23}}{\sqrt[3]{p}  }\cdot \sqrt[6]{p} + 2p^{-\frac 56} p^{\frac 43}} = ?$$um diesen Ausdruck zu vereinfachen, braucht man zunächst folgende Regeln:$$\sqrt[n]{x} = x^{\frac 1n} \\ x^0 = 1 \\ \frac 1{x^n} = x^{-n}\\  x^a \cdot x^b = x^{a+b}$$wobei \(x\) und \(n\) wiederum für beliebeige Ausdrücke stehen. Auf den obigen Term angewendet steht dann da:$$\frac{(p^2+2pq+q^2)^{\frac {a+b}{2a+2b}} - p \cdot 1}{p^{\frac  23 - \frac 13 + \frac 16}+ 2p^{-\frac 56 + \frac 43}}$$Jetzt kann man noch sehen, dass \(2a+2b = 2(a+b)\) ist, womit sich der Exponent im Zähler vereinfacht. Und weiter ist \(p^2+2pq+q^2=(p+q)^2\). Das und das Addieren der Brüche bringt$$\frac{(p+q)^{\frac 22} - p }{p^{\frac  12}+ 2p^{\frac 12}}$$und das ist$$\frac{(p+q)^{\frac 22} - p }{p^{\frac  12}+ 2p^{\frac 12}}=\frac{p }{3p^{\frac 12}} = \frac 13 p^{\frac 12} = \frac 13 \sqrt p$$