Überlagerung von Flächen auf Kreisbahn. Wie kommt die Formel zustande?

Question

Aufgabe:

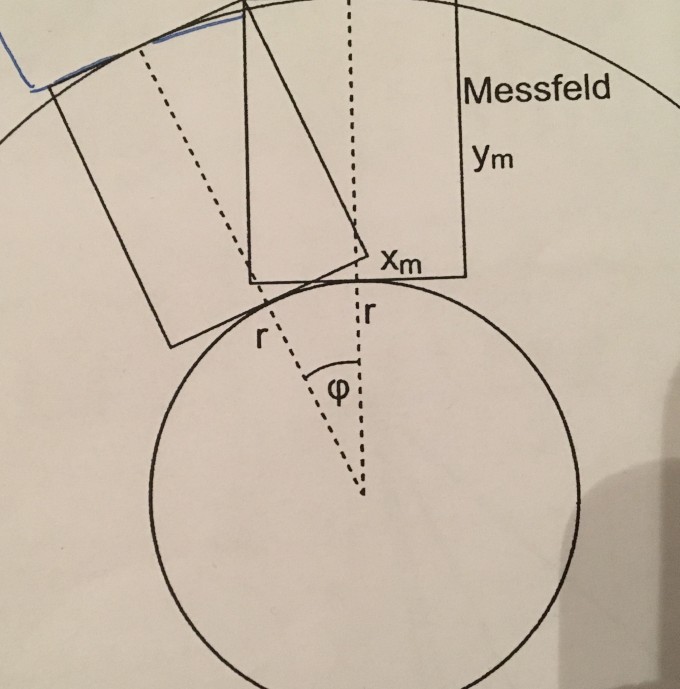
in dem Aufbau auf dem Foto geht es darum einen Winkel φ so zu ermitteln, dass 2 aufeinanderfolgende Fotos (Breite Xm, Höhe Ym) nach Durchlauf des Winkels so gemacht werden könnnen, dass dabei möglichst wenig Information verloren geht oder doppelt gemacht wird . Dabei soll diese Formel hier in Abhängigkeit von der Breite Xm des Fotos, einem Überlagerungsfaktor η und dem radius r gelten:

φ=2arctan(\(  η\frac{Xm}{2r} )\)  Für den Überlagerungsfaktor wird dabei η=0,9 angenommen

Problem/Ansatz:

Meine Frage lautet, wie man auf diese Formel kommt. Kann hier jemand erkennen, was genau hinter dieser Formel steckt bzw. welche Gesetzmäßigkeiten verwendet wurden?

Answer 1

Vielleicht so was:

Tangenten stehen senkrecht auf dem Kreis.

tan(phi/2) = a/r

phi/2 = arctan(a/r)

phi = 2arctan(a/r)

und a ist ein Vielfaches von xm/2 . Also a = η xm/2

Einsetzen:

phi = 2arctan( η * xm/(2r) )

Die blaue Winkelhalbierende von phi kannst du auch verlängern. Das "spitze" Viereck darüber ist zum eben betrachteten Viereck ähnlich.

Gleiche Überlegung zu tan(phi/2) ist auch dort möglich. Da kommt dann ym und (xm/2 - a) ins Spiel.

Answer 2

Hi

Was heißt denn ''so gemacht werden könnnen, dass dabei möglichst wenig Information verloren geht oder doppelt gemacht wird'' und was soll der Überlagerungsfaktor sein? Also habt ihr dafür ne Definition?

LG

Comments

Ich habe leider gar keine Definition, da ich diesen Arbeitsschritt einer anderen Person nachvollziehen muss ;) Beim Überlagerungsfaktor geht es wohl um eine Toleranz, inwieweit sich die Bilder überlappen dürfen... Nun ja bei einer Winkelveränderung zwischen 2 Fotos sollte natürlich zwischendurch möglichst wenig von der Kreisfläche nicht erfasst worden sein und es soll auf einem Foto auch nicht unnötig doppelte Information vorhanden sein, die auf dem anderen Foto ja schon erfasst wurde... also ein Kompromiss, eine Optimierungsgeschichte...

Es geht tatsächlich aber nur darum, diese Gleichung für den Winkel nachzuvollziehen

---

und was soll der Überlagerungsfaktor sein

vermutlich das Verhältnis der roten zur grünen Streckenlänge 

---

Und genau deswegen zweifel ich die Formel an.

Der Überlagerungsfaktor ist also unabhängig von ym. Was passiert wenn man einfach nur mal zum Spaß ym gegen unendlich gehen lässt. Für mein Verständnis müsste dann der Winkel φ immer kleiner werden, damit möglichst wenig Informationen verloren geht. Aber ne. Mit dem Winkel passiert nichts.