Hallo Pascal,
Es wird klarer, wenn man vom Mittelpunkt \(Z\) des Kreises die Lote auf die drei eingezeichneten Geraden (blau) fällt.
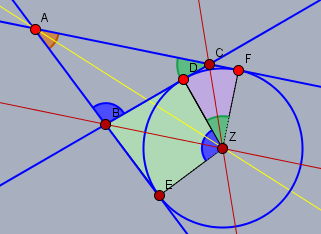
Es entstehen die Fußpunkte \(D\), \(E\) und \(F\). Die Vierecke \(BEZD\) und \(ZFCD\) sind Drachenvierecke mit rechten Winkeln (Lote) an den 'Ohren'. Da die Winkelsumme im Viereck \(=360°\) beträgt und die Ohren rechte Winkel sind, muss die Summe der gegenüber liegenden Winkel \(\angle EBD\) und \(\angle DZE\) (blau bei \(Z\)) gleich \(180°\) sein. Die Summe der Winkel \(\angle DCF\) und \(\angle FZD\) (grün bei \(Z\)) ist ebenso \(180°\).
Genauso ist die Summe der Nebenwinkel im Punkt \(B\) - also \(\beta = \angle CBA\) (blau bei \(B\)) und \(\angle EBD\) gleich \(180°\). Gleiches gilt für die Nebenwinkel bei \(C\). Daraus folgt, dass $$\begin{aligned}\angle DZE &= \angle CBA = \beta && \text{blau}\\ \angle FZD &= \angle ACB = \gamma && \text{grün}\end{aligned}$$Nun ist aber eine der Diagonalen im Drachenviereck auch gleichzeitig die Winkelhalbierende (rot). Daraus folgt, dass $$\begin{aligned} \mu &= \angle CZB = \frac 12 \angle DZE + \frac 12 \angle FZD \\ &= \frac 12 (\beta + \gamma) && \left|\, \alpha + \beta + \gamma = 180° \right. \\ &= \frac 12 (180° - \alpha) \\ & = 90° - \frac {\alpha}2\end{aligned} $$
Eine Alternative:
Schneiden sich zwei Geraden, so stehen die Winkelhalbierenden der Nebenwinkel senkrecht auf einander.
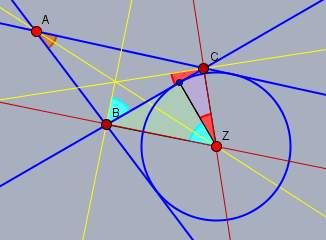
Im obigen Bild sind alle gelben und roten Geraden Winkelhalbierende. Die markierten Dreiecke (grün und violett) sind rechtwinklige. Daraus folgt, dass die beiden hellblauen Winkel und die beiden roten Winkel jeweils paarweise gleich sind. Aus der Summe des hellblauen und roten Winkels folgt dann $$\mu = \frac 12 \beta + \frac 12 \gamma = 90 - \frac {\alpha}2$$ Gruß Werner