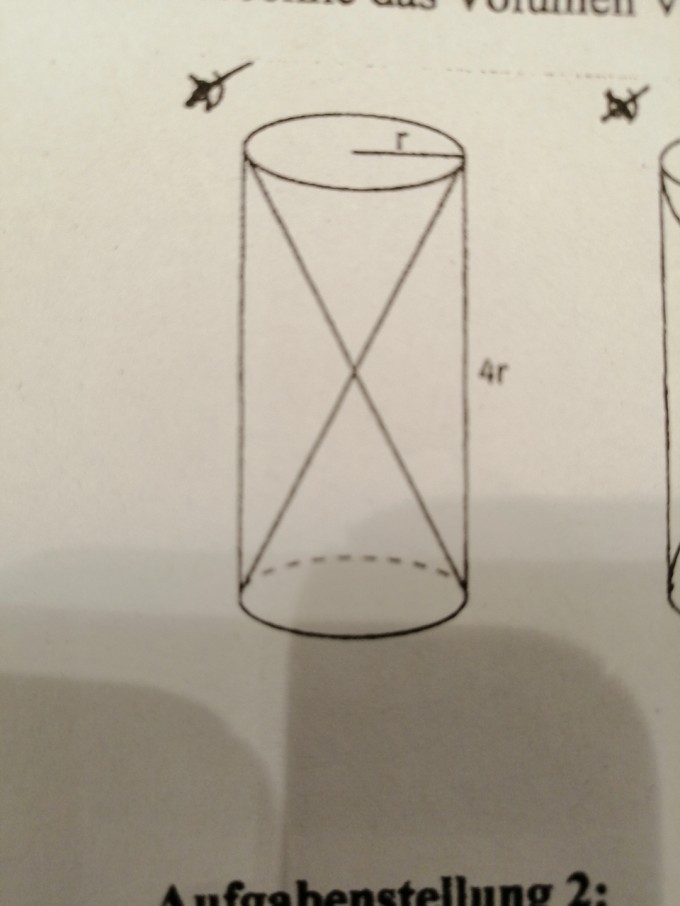
 Aufgabe:Es soll das Volumen V des einbeschriebenen Körpers und das des Restkörpers berechnet werden
Aufgabe:Es soll das Volumen V des einbeschriebenen Körpers und das des Restkörpers berechnet werden
Hinweis: h = 4r (ist auf dem Bild nicht gut zu erkennen)
Problem/Ansatz: V (Innenkörper) = 2 * (1/3 * π * r² *h)
= 2 * (1/3 * π *r² * 2r)
= 2/3 * 2π * 2r² * 4r)
= 33,51r³
Dass das stimmt, glaube ich zwar nicht, aber ich weiß auch keinen anderen Ansatz und habe vor diesem Hintergrund erst einmal auf die Berechnung des Restkörper-Volumens verzichtet.