(Antwort korrigiert; der Zenitwinkel war falsch)
Wie rechnet man das aus?
Eine Skizze ist der Anfang von allem ...
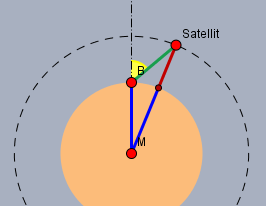
Die blauen Strecken sind der Erdradius \(R\). Die rote ist die Höhe \(h\) des Satelliten über der Erdoberfläche. Der gelbe Winkel ist der Zenitwinkel unter dem der Satellit dem Beobachter bei \(B\) erscheint. Und die grüne Strecke \(x\) ist gesucht.
Die vier Streckenstücke bilden ein Dreieck mit einem bekannten Winkel. Da eignet sich der Cosinussatz:$$\begin{aligned}(R+h)^2&= R^2 + x^2 - 2Rx\cos(180°-50°) \\ \implies 0&= x^2 - 2 \cdot 6370 \text{km} \cdot \cos(130°) - (2 \cdot 6370 \text{km} \cdot 100 \text{km} + 100^2 \text{km}^2) \\ \implies x_{1,2}&\approx -4094 \text{km} \pm 4248 \text{km} \end{aligned}$$Das negative Ergebnis gibt keinen Sinn. Es bleibt: $$x \approx 154 \text{km}$$Gruß Werner