Stereometrie: Gleichungssystem Berechnungen in Halbkugel und Kegel

Question

Aufgabe:

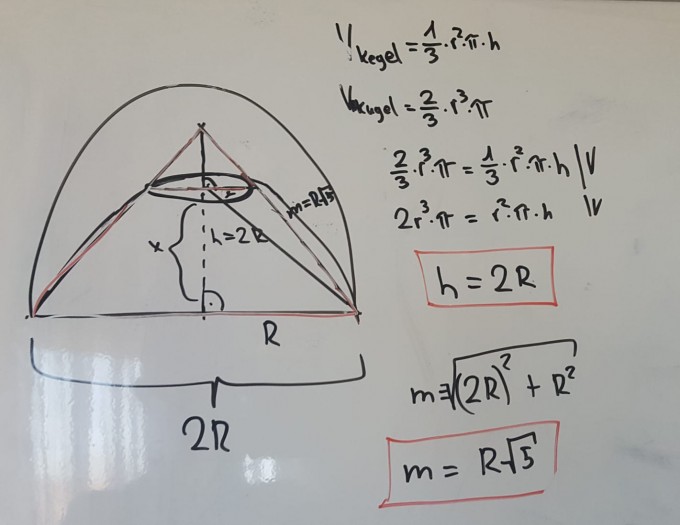
Eine Halbkugel und ein gerader Kegel haben dieselbe Grundkreisfläche mit Radius r und auch dasselbe Volumen. In welchem Abstand zum Grundkreis durchdringt der Kegelmantel die Oberfläche der Halbkugel und wie gross ist der Schnittkreisradius?

Problem/Ansatz:

Ich konnte die beiden Volumina gleichsetzen und die Höhe des Kegels berechnen, die lautet: 2r.

Aber das sind typische Aufgaben mit Verhältnis und Gleichungssystem, wo ich einfach nie den Überblick habe. Ich verstehe einfach nicht, wie ich sowas am besten berechnen soll. Ich habe auch diese Skizze dazu angefertigt und weitere Werte:

Bei meiner Skizze ist R der Radius der beidem Figuren.

Bei meiner Skizze ist r der Schnittkreisradius.

Ich hoffe, dass mir jemand einen geeigneten Weg zeigen kann, wie ich bei solchen Aufgaben vorgehen sollte.

Answer 1

MS  =  h_Kegel  = 2R

Man hat die Gleichungen:

x + y = 2R   ;   x² + r² = R²   und  R / r = (x+y) / y  [ 2. Strahlensatz (oder Ähnlichkeit ]

.......

Ich erhalte den gesuchten Abstand  x = 4/5 · R

Gruß Wolfgang

Comments

wtf? Wieso habe ich das nicht gesehen. Hää, das ist ja gar nicht so schwierig.

---

Danke dir so sehr!

---

immer wieder gern :-)

Answer 2

Wähle den Grundkreisradius als Längeneinheit (R=1):

Mache einen ebenen Schnitt entlang der Kegelhöhe. Dann ist die Kegelhöhe h=2. Die Gerade mit der Gleichung (1) y=2x+2 schneidet den Einheitskreis mit der Gleichung (2) x²+y²=1 in (x|y). Zur Bestimmung von (x|y) löse das System aus den Gleichungen (1) und (2). Dann ist x·R der gesuchte Schnittkreisradius und y·R der gesuchte Abstand.

Comments

Ahm, ich verstehe nicht wie du das meinst.

Ich habe verstanden, dass du das R durch 1 ersetzt hast, aber wie kommst du auf y = 2x +2 und x^2+y^2 = 1????

Wir müssen das mit Ähnlichkeit lösen glaube ich mal, so haben wir es immer gemacht. Oder mit Verhältnis.

---

Du musst dich in meine Lage hineinversetzen. Mit dieser Erklärung kann ich doch nichts anfangen.

---

Ich denke, Wolfgangs Erkärung genügt.

Answer 3

Hier zunächst eine Skizze.

Es gilt den Schnittpunkt zwischen Kreis und Außenlinie Kegel
( rot ) zu berechnen.

Für die Kreisgleichung gilt
r^2 = x^2 + y^2 ( Pythagoras )
y = √ ( r^2 - x^2 )
Die Kegelaußenlinie ist eine Gerade mit Steigung
h = 2r
m = 2r / r = 2
y-Achsenabschnitt = 2r
y = 2 * x + 2r

Schnittpunkt
√ ( r^2 - x^2 ) = 2x + 2r
x = - 3/5 * r
Eingesetzt
y ( -3/5 r ) = 2 * (-3/5 * r ) + 2r
y =  4/5 * r

( -3/5 * r | 4/5 * r )