Praktische Anwendungsaufgabe. Weg-Zeit-Funktion.

Question

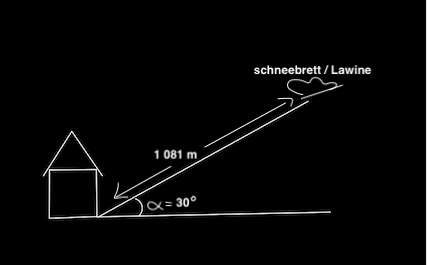
"Am Fuße eines Berghanges mit dem Neigungswinkel α = 30° steht ein Hause. 1 081 m längs des Hanges entsteht ein Schneebrett, welches beim Hinunterlegen zu einer Schneelawine entwickelt. Diese bewegt sich auf ein schiefen Berghang hinunter nach der Weg-Zeit-Funktion

s(t) = 0,5 • (sin α) • g • t²

wobei α = 30° und g die Fallbescheinigung 9,81 m/s² sind."

Aufgabenstellung:

"a) Geben Sie die Funktionsgleichung für diesen konkreten Fall an. Welchen Weg hat die Lawine in den ersten 5 Sekunden zurückgelegt?

b) Nach welcher Zeit hat sie das Haus erreich?

c) Geben Sie die Durchschnittsgeschwindigkeit im Zeitintervall [t₁ ; t₂] allgemein an und berechnen Sie diese in den ersten 5 Sekunden nach der Erstehung der Lawine und in den letzten 5 Sekunden vor dem Aufprall auf das Hause.

d) Geben Sie die Momentangeschwindigkeit der Lawine allgemein zum Zeitpunkt t₀ an und berechnen Sie diese nach 5 Sekunden, nach 10 Sekunden und zum Zeitpunkt des Aufpralls auf das Haus."

Ich komme nicht zurecht... ich bin mir nicht genau sicher was ich in die Formel wo eingeben soll... konnte jemand mir hierbei bitte helfen??

Comments

Was ist mit Aufgabe e!

Die verstehe ich nicht!

Gib die Funktionsgleichung der Funktion an, die die Geschwindigkeit in Abhän- gigkeit von der Zeit beschreibt.

Bitte Hilfe

---

e.) gibt es in der Fragestellung nicht.
Meintest du die Aufgabe d.) ?

d.)
s = Strecke in m
Weg / Zeitzusammenhang
s ( t ) = 2.4525 * t^2
1.Ableitung
Geschwindigkeit / Zeitzusammenhang
s ´ = v = ( Momentan-) Geschwindigkeit in m/s
s ´ ( t ) = ( 2.4525 * t^2 ) ´
v ( t ) = 2.4525 * 2 * t
v ( t ) = 4.85 * t

v ( 5 ) = 4.85 * 5 m/s = 24.25 m/s
v ( 10 ) = 4.85 * 10 m/s
v ( 22.11 ) = 4.85 * 22.11 m/s

---

Nein! Kann du mir mit der Frage helfen bitte!

Es geht um eine die gleich Aufgabe wie oben nur diese Frage!

Gib die Funktionsgleichung der Funktion an, die die Geschwindigkeit in Abhän- gigkeit von der Zeit beschreibt.

---

Das habe ich dir jetzt schon 2 mal mitgeteilt :
Die Momentanbgeschwindigkeit als Funktion
der Zeit ist gleich 4.85 * Zeit.

v ( t ) = 4.85 * t

Answer 1

"a) Geben Sie die Funktionsgleichung für diesen konkreten Fall an.
Steht schon in der Aufgabe
s(t) = 0,5 • (sin α) • g • t^2
alpha = 30 °
sin ( alpha) = 0.5
g = 9.81 m/s^2
t = Zeit in sec
t^2 : das Quadrat der Zeit
s(t) = 0,5 • (sin α) • g • t^2
s(t) = 0,5 • 0.5 • 9.81 • t^2
s ( t ) = 2.4525 * t^2
Welchen Weg hat die Lawine in den ersten 5 Sekunden zurückgelegt?
s ( 5 ) = 2.4525 * 5^2 = 60.625 m

b) Nach welcher Zeit hat sie das Haus erreicht?
s ( t ) = 2.4525 * t^2 = 1081 m
t^2 = 1081 / 2.425
t = √ (1081 / 2.425 )
t = 21.11 sec

c) Geben Sie die Durchschnittsgeschwindigkeit im Zeitintervall [t1 ; t2] allgemein an und berechnen Sie diese in den ersten 5 Sekunden nach der Erstehung der Lawine und in den letzten 5 Sekunden vor dem Aufprall auf das Hause.

Durchschnittsgeschwindigkeit =
Δ s / Δ t =
[ s ( ende ) minus s ( anfang ) ] / [ t ( ende) minus  t (anfang ) ]
[ s ( t2 ) - s ( t1 ) ]  /  ( t2  -  t1 )

[ s ( 5 ) - s ( 0 ) ]  /  ( 5  -  0 )
[ s ( 21.11 ) - s ( 21.11 - 5 ) ]  /  ( 21.11  -  ( 21.11 - 5 ) )

d) Geben Sie die Momentangeschwindigkeit der Lawine allgemein zum Zeitpunkt t0 an und berechnen Sie diese nach 5 Sekunden, nach 10 Sekunden und zum Zeitpunkt des Aufpralls auf das Haus."

s´( t ) = v ( t ) = ( 2.425 * t^2 ) ´
v ( t ) = 4.85 * t

v ( 5 ) =
v ( 10 ) =
v ( 22.11 ) =

Comments

Wow! Vielen Dank auf deine Antwort! :) Ich habe alles nachvollziehen und nachrechnen können! Nur bei c) bin ich nicht sicher, ob

"[ s ( 21.11 ) - s ( 21.11 - 5 ) ]  /  ( 21.11  -  ( 21.11 - 5 ) )"

die fertige Antwort ist, oder ob ich es noch mehr ausrechnen soll... 

und bei d):
Für was steht V? 
Ansonsten Habe ich alles verstanden!

Nochmals vielen vielen Dank!

---

c) Geben Sie die Durchschnittsgeschwindigkeit im Zeitintervall [t1 ; t2] allgemein an und berechnen Sie diese in den ersten 5 Sekunden nach der Erstehung der Lawine und in den letzten 5 Sekunden vor dem Aufprall auf das Hause.

s ( t ) = 2.4525 * t2

[ s ( 5 ) - s ( 0 ) ]  /  ( 5  -  0 )
s ( 5 ) = 61.3125 m
s ( 0 ) = 0 m
v  = ( 61.3125 - 0 ) / ( 5 - 0 )
v = 12.2625 m/s

[ s ( 21.11 ) - s ( 21.11 - 5 ) ]  /  ( 21.11  -  ( 21.11 - 5 ) )
s ( 21.11 ) = 1092.
s ( 16.11 ) = 636.50
( 1092 - 636.5 ) / ( 21.11 - 16.11)
455.5 / 5
91.1 m/s

d.)
s = Strecke in m
1.Ableitung
s ´ = v = ( Momentan-) Geschwindigkeit in m/s

v ( t ) = 4.85 * t
v ( 5 ) = 4.85 * 5 m/s = 24.25 m/s
v ( 10 ) = 4.85 * 10 m/s
v ( 22.11 ) = 4.85 * 22.11 m/s

Answer 2

a) Geben Sie die Funktionsgleichung für diesen konkreten Fall an. Welchen Weg hat die Lawine in den ersten 5 Sekunden zurückgelegt?

sin(30°)=1/2

s(t) = 0,5 • 1/2 • 9,81 • t² =2,4525·t²

s(5)=2,4525·25=61,3125

In den ersten 5 Sekunden hat die Lawine etwa 61 m zurückgelegt?