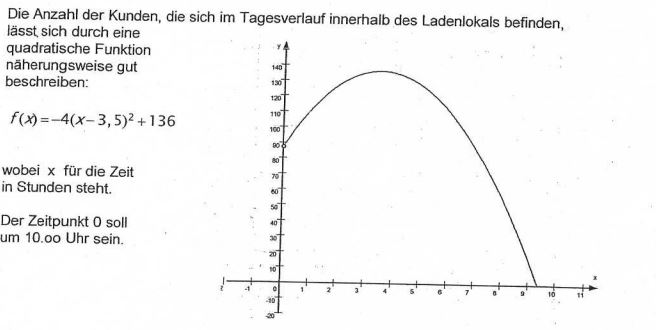
vielleicht kann mir wer bei dieser Aufgabe helfen.
a) Berechnen Sie, wie viele Kunden sich um 10 Uhr im Ladenlokal befinden,
b) Ermitteln Sie die maximale Anzahl von Kunden im Ladenlokal und geben Sie die dazugehörige Uhrzeit an.
c) Berechnen Sie die Uhrzeiten, zu denen sich genau 120 Kunden im Laden befinden.
d) Berechnen Sie die Uhrzeit, zu der sich keine Kunden im Laden mehr befinden
e) Am folgenden Verkaufstag lässt der Kundenandrang nach. Die Anzahl der Kunden kann durch h(x)=6x(x-8) beschrieben werden, wobei x wiederrum für die Zeit in Stunden steht. Der Zeitpunkt 0 soll ebenfalls um 10 Uhr sein.
Begründen Sie, dass der Kundenantrang im Vergleich zum Vortag zu jeder Uhrzeit geringer ist.