Die b-adische Entwicklung durch geometrische Reihe

Question

Leider komme ich mit dem derzeitigen Übungsblatt überhaupt nicht zurecht, könnte mir jemand bitte die Lösung zu folgender Aufgabe nennen. Ich weiss nämlich überhaupt nicht wie ich an diese hier ran gehen soll...

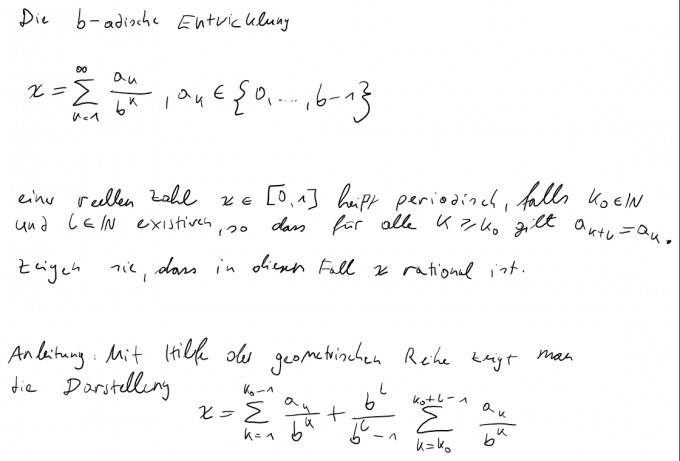
Die b-adische Entwicklung $$\chi = \sum_{k=1}^{\infty} \frac{a_k}{ b^k}, \quad a_k \in \{ 0, \, \dots,\, b-1\}$$einer reellen Zahl \(\chi \in [0,\,1]\) heißt periodisch, falls ein \(k_0 \in \mathbb{N}\) und ein \(l \in \mathbb{N}\) existiert, so dass für alle \(k \ge k_0\) gilt \(a_{k+l} = a_k\).

Zeigen Sie, dass in diesem Fall \(\chi\) rational ist.

Anleitung: mit Hilfe der geometrischen Reihe zeigt man die Darstellung$$\chi = \sum_{k=1}^{k_0-1} \frac{a_k}{ b^k} + \frac{b^l}{b^l - 1} \sum_{k=k_0}^{k_0+l-1} \frac{a_k}{ b^k}$$

Comments

Weiß niemand zu helfen ?

---

Vom Duplikat:

Titel: Zeigen Sie, dass in diesem Fall x rational ist

Stichworte: beweis

Aufgabe:

Die b-adische Entwicklung
x =∑ak/bk
k=1 bis n, ak ∈ {0, ..., b − 1}
einer reellen Zahl x ∈ [0, 1] heißt periodisch, falls k0 ∈ N und l ∈ N existieren, so dass für
alle k ≥ k0 gilt ak+l = ak. Zeigen Sie, dass in diesem Fall x rational ist.

---

Hallo

 zu der Aufgabe gab es den entscheidenden Hinweis, warum teilst du den nicht mit, oder warum verwendest du ihn nicht?

Gruß lul

Answer 1

Hallo zuerst den vorperiodischen Anteil berechnen, der ist ko-1 lang das ist die erste Summe , danach die Länge der Periode l also hat man (ak0*/b^k0+a_k0+1/b^k0+1+... a_k0+l-1b^k0+l-1) das schreibt man als Summe S  das ist deine zweite Summe. wenn man die jetzt mit 1/b^l multipliziert, hat man die nächste Periode usw, unendlich oft dann hast du die Summe von 1/b^kl*S von k=0 bis oo das steht da. S ist rational da ja nur eine endliche Summe von Brüchen, die vorperiode auch und die Summe über (1/b^l)^k auch. Also steht eigentlich schon alles da.

Gruß lul