Der „Römische Verbund“ ist die vollständige Parkettierung der Ebene mit zwei verschieden großen quadratischen Fliesen, eines kongruent zu QRST und eines kongruent zu USVW.
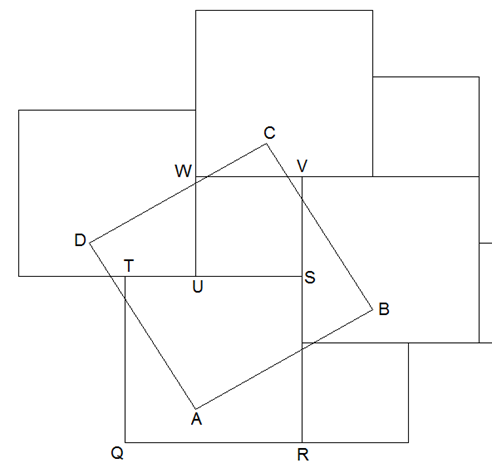
Auf diesen Römischen Verbund wird ein Quadrat ABCD gelegt mit AB parallel zu TV sowie AB und TV gleichlang aber sonst ann die Lage von ABCD vollkommen beliebig gewählt werden. Mit einer derartigen Grundkonstruktion kann bei jeder Lage von ABCD ein anschaulicher Beweis des Satzes von Pythagoras erfolgen:
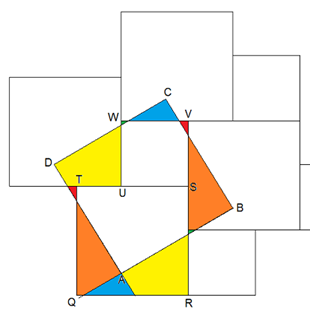
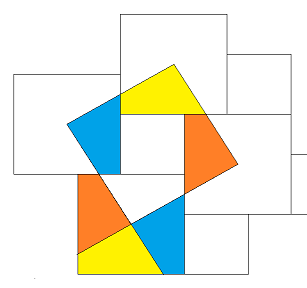
Die Linien des Römischen Verbundes und die verlängerten Seiten des Quadrates ABCD zerlegen den Römischen Verbund in Teilflächen. Jede Fläche innerhalb der Quadrate QRST und USVW findet eine kongruente Entsprechung innerhalb des Quadrates ABCD. Für besondere Lagen der Punkte A, B, C und D ergeben sich häufig vorgeführte Pythagorasbeweise, so zum Beispiel, wenn A Mittelpunkt von QRST ist:
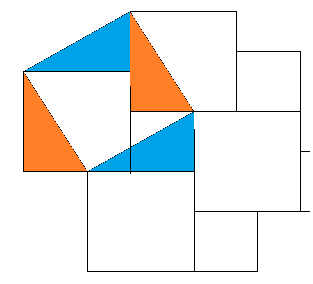
Ein anderer „klassischer“ Pythagorasbeweis entsteht, wenn A auf T liegt (Anmerkung: In der Darstellung wurde die Fliese QRST durch eine andere dazu kongruente Fliese ersetzt):
Bei Verwendung des Römischen Verbundes zum Beweis des Satzes von Pythagoras gibt es für jede Lage des Quadrates ABCD einen anschaulichen Pythagorasbeweis und damit als unendlich viele. Vor diesem Hintergrund wird die Aussage „Zum Satz des Pythagoras existieren mehr als 400 verschiedene Beweise“
http://www.schule-bw.de/faecher-und-schularten/mathematisch-naturwissenschaftliche-faecher/mathematik/unterrichtsmaterialien/sekundarstufe1/geometrie/pyth/beweise
zwar bestätigt aber gegenstandslos.