Bedingte Wahrscheinlichkeit - die neunte aufgedeckte Karte das zweite aufgedeckte Ass ist

Question

Die Aufgabe:

Unter 32 Karten befinden sich vier Asse. Die Karten werden gemischt und nacheinander aufgedeckt.
Wie groß ist die Wahrscheinlichkeit, dass die neunte aufgedeckte Karte das zweite aufgedeckte Ass ist?

Mein Lösungsansatz:

A = "Unter den ersten acht Karten ist ein As"

B = "Die neunte Karte ist ein As"

Wir suchen P(A ∩ B) = P(A) * P(B|A)

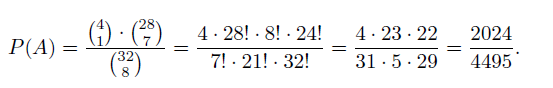
Meine Frage ist, wie ich nun P(B|A) erhalte? Das Ereignis P(B) weiß ich ja nicht, deshalb verwende ich P(B|A). Es wäre sehr nett, wenn mir jemand sagen würde wie ich P(B|A) erhalte.

Ich würde mich sehr über eine Antwort freuen. Vielen Dank im Voraus.

Euer Max

Comments

Antwort zurück gezogen.

Answer 1

Wenn unter den ersten acht Karten genau ein Ass ist, dann kann die neunte Karte aus 32-8 Karten ausgewählt werden, von denen 3 Asse sind. P(B|A) = 3/(32-8)

Comments

Also an der der 9. Ziehung sind es ja nur noch 3 Asse übrig. Das heißt ich habe doch eine Wahrscheinlichkeit von

(3 über 1 * 24 über 23) / 24 über 1

Vielleicht ist mein Gedanke auch falsch.

dann kann die neunte Karte aus 32-8 Karten ausgewählt werden, von denen 3 Asse sind.

Wieso das? Ich hoffe du kannst mir weiterhelfen.

---

(3 über 1 * 24 über 23) / 24 über 1

Mit welcher Formel hast du das berechnet?

dann kann die neunte Karte aus 32-8 Karten ausgewählt werden, von denen 3 Asse sind.

Die neunte Karte kann aus 32-8 Karten ausgewählt werden, weil ursprünglich 32 Karten zur Verfügung stehen, aber 8 Karten schon aufgedeckt wurden.

Es sind nur noch 3 Asse, weil ursprünglich 4 Asse vorhanden sind, aber ein Ass schon aufgedeckt wurde.

---

Mit welcher Formel hast du das berechnet?

Ich habe mir das ausgedacht.

Also heißt das im Prinzip beachte ich nicht wirklich, ob es jetzt die 9 Stelle oder n-te Stelle ist? Sondern ich gucke einfach was die Wahrscheinlichkeit ist ein As aus den 32 Karten zu erhalten?

---

beachte ich nicht wirklich, ob es jetzt die 9 Stelle oder n-te Stelle ist?

Doch, das tust du. Die Stelle hat Einfluss darauf, aus wie viel Karten du auswählst.

Answer 2

Du kannst P(B) doch berechnen:

P(ein Ass unter den ersten 8 Karten) = (4*28*27*26*25*24*23*22)/(32*31*30*29*28*27*26*25) *(8über1)

oder: (4über1)*(28über7)/(32über4)

Comments

(4über1)

Wieso sind es nicht 3 über 1 ? Hätte gedacht, es sind nur noch 3 Asse im Spiel, oder ist des zu dem Zeitpunkt nicht richtig?

(28über7)

Sind jetzt nicht 32 - 8 = 24 Karten nur noch Übrig?

(32über4)

Oder muss ich allgemein schauen, dass ich ein As aus den 4 Assen erhalte? Und nicht exakt sagen muss das dass neunte Ass das zweite ist?

---

Unter den ersten 8 Karten muss irgendeins der 4 Asse sein.

Alle anderen 7 dürfen kein Ass sein.