Wahrscheinlichkeitsrechnung Baumdiagramm Problem

Question

Die Aufgabe: In einer urne befinden sich 1 weiße, 2 rote und 3 schwarze kugeln. Man zieht nacheinander zwei kugeln einmal ohne zurücklegen und einmal mit zurücklegen der kugel nach jedem zug. zeichne jeweils ein baumdiagramm und gib einen ergebnisraum und seine Mächtigkeit an. Berechne die Wahrscheinlichkeit, dass folgendes ereignis eintritt" a) P (w, r). b) P (r, r) und c) P (r, r) nun meine frage, zum beispiel bei P (w, r) muss ich ja weiß und rot ziehen. also : 1/6 mal 2/6. muss ich das nur einmal machen oder alle Möglichkeiten wo rot und weiß ist?

Answer 1

Hallo Dilara, 

ich habe Dir mal zwei kleine Baumdiagramme gezeichnet. 

Mit Zurücklegen:

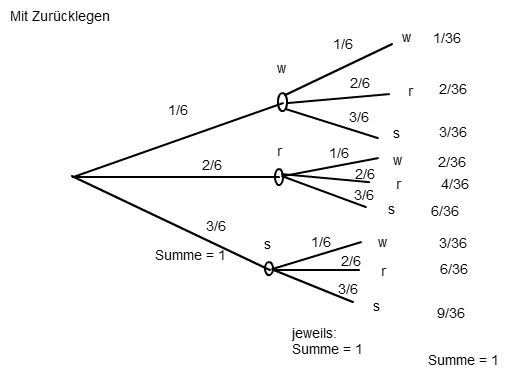
Ohne Zurücklegen:

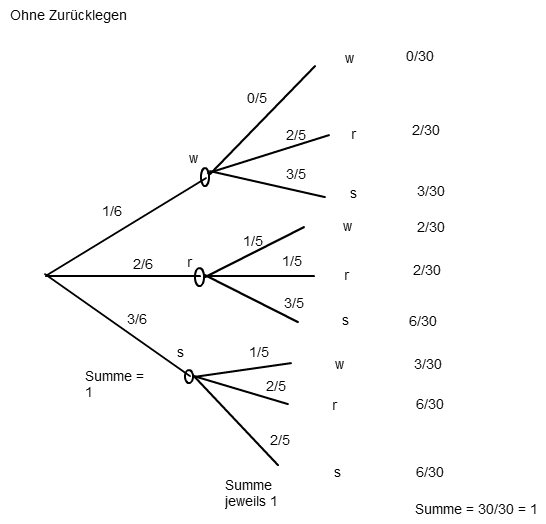
Die Frage ist jetzt, ob die Reihenfolge der Ziehung von Bedeutung ist; bei der Aufgabenstellung vermute ich, dass die Reihenfolge von Bedeutung ist.

 

Wenn ja, so gehst Du nur den Pfad, der dem Ereignis entspricht, entlang und notierst die Wahrscheinlichkeit, 

zum Beispiel: 

P (w, r) mit Zurücklegen = 2/36 = 1/18

P(w, r) ohne Zurücklegen = 2/30 = 1/15

 

Sollte allerdings entgegen meiner Vermutung die Reihenfolge keine Rolle spielen, so müsstest Du sämtliche Pfade, die dem Ereignis entsprechen, abschreiten und die Wahrscheinlichkeiten addieren.

Zum Beispiel: 

P (w und r) mit Zurücklegen = 2/36 + 2/36 = 4/36 = 1/9

P (w und r) ohne Zurücklegen = 2/30 + 2/30 = 4/30 = 2/15

 

Besten Gruß

Comments

fein. :-)

da du schneller warst, kann ich mein baumdiagramm wieder löschen :D

---

@ gorgar:
Tut mir Leid, dass Du Dir die Mühe umsonst gemacht hast!

Ich kenne das: Mir macht öfters meine Uralt-Möhre von PC einen Strich durch die "Rechnung" :-)

---

ist okay, das braucht dir nicht leid zu tun! :-)

schade, dass man hier nicht sehen kann, ob bereits jemand an der antwort arbeitet.

machbar wäre das jedenfalls, das kenne ich auch einem anderen forum.

---

dankeschön! :) aber das ist halt die ganze aufgabe, nur das steht da, jetzt weiss ich selber nicht ob die Reihenfolge von bedeutung ist.. danke! liebe grüße

---

@gorgar: Vielleicht wäre deine Antwort für DilaraBooth noch besser gewesen? Vielleicht hättest du einen anderen Weg aufgezeigt? Und dadurch die "Beste Antwort" erhalten...

Die technische Implementierung, wer eine Frage gerade beantwortet, ist nicht ohne Weiteres möglich. Wenn du Nachfragen hierzu hast, bitte hier posten: https://www.mathelounge.de/chat

Schöne Grüße :)
Kai

---

@ DilaraBooth:

Gern geschehen !!

Ich kann mich nur wiederholen :-)

Ich glaube, dass die Reihenfolge hier wirklich von Bedeutung ist: P(w, r) zum Beispiel klingt sehr danach. Sollte sie nicht von Bedeutung sein, würde ich als Fragesteller P(w und r) oder etwas Ähnliches schreiben.
Wenn so etwas in einer (wichtigen) Arbeit vorkommt, kannst Du ja auf Nummer Sicher gehen und schreiben:

"Ich interpretiere die Aufgabe so, dass die Reihenfolge von Bedeutung ist (also erst w und dann r); dann ergibt sich eine Wahrscheinlichkeit von ..., andernfalls, falls gemeint ist, genau eine weiße und eine rote Kugel, dann ergibt sich eine Wahrscheinlichkeit von ... "

Mehr kann man wohl kaum machen :-(

Besten Gruß