Tilgung Annuität Formel t

Question

Aufgabe:

Eine Bank gewährt einen Kredit von 200000€ mit dem Schuldner: Der Kredit ist mit 10% zu verzinsen und anfänglich mit 16% zu tilgen, wobei die Annuität konstant sein soll.

Problem/Ansatz:

a) na wie viel Jahren ist die Hälfte des Darlehens getilgt?

b) berechnen Sie die Annuität im Jahr 10

Welche Formeln muss ich dafür verwenden?

Answer 1

a) Annuität = 200000*(0,1+0,16) = 52000

200000*1,1^n = 52000*(1,1^n-1)/0,1

n= 5,09 Jahre (Gesamtdauer)

200000*1.1^n -52000*(1,1^n-1)/0,01 = 100000

...

Die Aufgabe macht so keinen Sinn,weil der Kredit nur 5 Jahre läuft.

Überprüfe deine Angaben! Soll Tilgung konstant sein? Das wäre logischer.

Comments

Die Aufgabe ist richtig.

a) Welche Laufzeit hat dieser Kredit?

b) Nach wie viel Jahren ist die Hälfte des Kredits gedeckt?

c) Wie hoch ist die Annuität im 10. Jahr?

a)

log(0 ,1 +0,16/0,1)/Log(1,1)=10

bei a habe ich 10 Jahre raus und deshalb muss es ja auch im Jahre 10 eine Annuität geben. Tilgung ist definitiv nicht konstant

---

Welche Annuität hast du raus? Bitte Rechenweg posten!

Was soll an meiner Annuität falsch sein? Sie kann nur 52000 betragen bei diesen Angaben und ändert sich nicht.

---

Annuitat habe ich die Gleiche raus.

Bloß mit geht es ja darum, wann die Hälfte des Kredits gedeckt ist und wie Hoch die Annuität im letzten Jahr ist bezogen auf a

---

Wo liegt den deiner Meinung der Fehler im Folgenden Tilgungsplan?

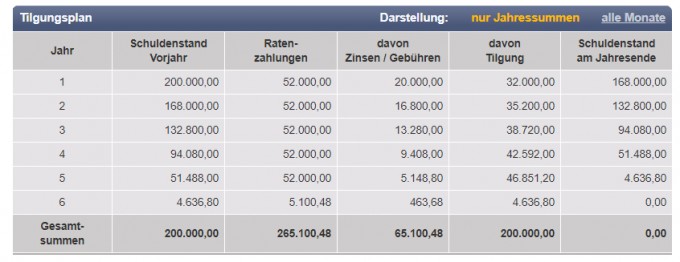
Zinssatz 10%, Anfängliche Tilgung 16%

Und deine Formel kann ich auch nicht so nachvollziehen. Gilt nicht

n = LN(R/(R - Bn·(q - 1))) / LN(q)

n = LN(52000/(52000 - 200000·(1.1 - 1))) / LN(1.1) = 5.094

Es sieht so aus als wolltest du durch den Barwert kürzen.

n = LN((0.1 + 0.16)/((0.1 + 0.16) - 1·(1.1 - 1))) / LN(1.1) = 5.094

n = LN((0.1 + 0.16)/((0.1 + 0.16) - 0.1)) / LN(1.1) = 5.094

n = LN((0.1 + 0.16)/(0.16)) / LN(1.1) = 5.094

---

c) Wie hoch ist die Annuität im 10. Jahr?

Aufgabe c) macht also so keinen Sinn. Bitte stelle die Aufgabe vollständig und richtig. Ändere nicht eigenmächtig irgendwelche Fragestellungen ab.

---

Wenn die Annuität immer gleich bleibt, beträgt sie auch im 10. Jahr 52000.

Es ergibt sich ein Widerspruch! Verstehst du, was ich meine?

Bei dieser Annuität ist der Kredit nach 5,09 Jahren abbezahlt.

---

Ja, scheinbar gibt es keinen.

Habe auch gesehen, dass ich mich verrechnet habe, bei den Jahren.

Ich habe: n=Log(p+s/s)/log (s)

Da komme ich jetzt auch auf 5,09jahre.

Muss ich für die Hälfte des Kredits bezüglich n denn einfach 5,0939/2 rechnen?

---

Ja, das verstehe ich, aber oft ist die letzte annuitAn ja doch eine andere, obwohl sie davor Konstant war und das verstehe ich nicht

---

Du musst unterscheiden zwischen konstanter Tilgungsrate und konstanter Annuität.

Dem Aufgabensteller muss ein Fehler unterlaufen sein.

---

Die letzte Annuität kann natürlich abweichen, siehe in dem obigen Tilgungsplan. In diesem Fall weicht die Annuität im 6. Jahr ab, weil dort nur noch der Rest zuzüglich Zinsen zu bezahlen ist.

---

Dankeschön, soweit habe ich alles verstanden, bis auf eines. Das mit der konstanten Annuität und nicht konstant war mir gar nicht bewusst.

Muss ich für die Hälfte des Kredits bezüglich n denn einfach 5,0939/2 rechnen?

---

Ist das nun so richtig, wie ich denke?

---

Nein. Schau  mal in meinen 1. Beitrag. Dort steht der Ansatz. :)

---

Das verstehe ich nicht. Da steht doch nur die Laufzeit

---

Ist das nun so richtig, wie ich denke?

Bitte stelle einfach mal die komplette Aufgabe vollständig und richtig.

Du möchtest doch sicher verlässliche Informationen und nicht nur ein rumgerate.

---

200000*1.1^n -52000*(1,1^n-1)/0,01 = 100000

Löse nach n auf!

---

Dankeschön :)