Der Hohlraum eines Glases

Question

Aufgabe:

Der Hohlraum eines Glases entsteht,indem sich die Parabel y=(2/3)x^2 um die y-Achse dreht.

Problem/Ansatz:

Wie viel Wasser ist enthalten ,wenn dass Glas bis zu einer Höhe von 6 cm gefüllt ist?

In welcher Höhe müsste die Markierung für 1/16 Liter angebracht sein?

Ich bitte um Hilfe,

Leider habe ich keine Antwort im Buch

Comments

Leider habe ich keine Antwort im Buch

Dein Ernst?! Denk doch mal über den Sachverhalt nach, ohne gleich zu verlangen, dass Jemand anderes deine Aufgaben macht. Ein Lösungsansatz zu bringen ist besser!

Answer 1

V = pi * Integral von 0 bis 6 über x^2 dy

  =  pi * Integral von 0 bis 6 über 1,5y  dy

   = pi * 27 ≈ 84,8 cm^3 .

Für den anderen Teil benutze

1/16 = pi * Integral von 0 bis h über 1,5y  dy

Answer 2

y = (2/3) *x^2
Um die y-Achse drehen kann ich nicht.
Ich drehe immer die Umkehrfunktion um die x-Achse.
x = (2/3) * y^2
3 / 2 * x = y^2
y = √ ( 3 / 2 * x )

y = f ( x ) ist der Funktionswert an der Stelle x
und ist der Radius des Glases.

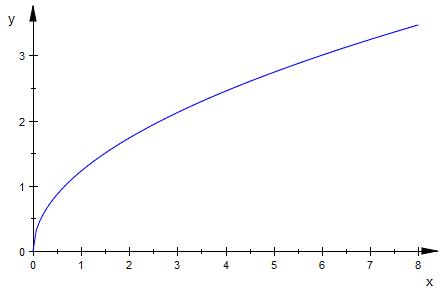
f ( x ) = r = √ ( 3 / 2 * x )
Rotationsfläche
A ( x ) = r ^2 * pi = ( 3/2 ) * x * pi
Stammfunktion
S ( x ) = ∫ ( 3/2 ) * x * pi dx
S ( x ) = ( 3/2 ) * x^2 / 2 * pi dx
S ( x ) = pi * 3/4 * x^2
Volumen
V ( x ) = [ S ] zwischen 0 und 6
( pi * 3/4 * 6^2 ) - ( pi * 3/4 * 0^2 )
V = 27 * pi

1/16 liter = 1/16 * 1000 cm^3

1000 / 16 = S ( x ) = pi * 3/4 * x^2
x = 5.15 cm