Eine allgemeine lineare Funktion ist eine Funktion der Form
$$f(x)=mx+n$$
Du weißt, dass deine Funktion die y-Achse schneidet, d.h (n>3).
$$P_1(0|n)$$
Zudem ist gegeben:
$$P_2(2|3)$$
Demzufolge:
$$m=\frac{ Δf(x)}{ Δx}=\frac{3-n}{2-0}=\frac{3-n}{2}$$
Einsetzen in f(x) liefert:
$$f(x)=\frac{3-n}{2}*x+n$$
Nullstellenberechnung führt zu:
$$f(x)=0=\frac{3-n}{2}*x_0+n$$
$$-n=\frac{3-n}{2}*x_0$$
$$x_0=-\frac{2n}{3-n}$$
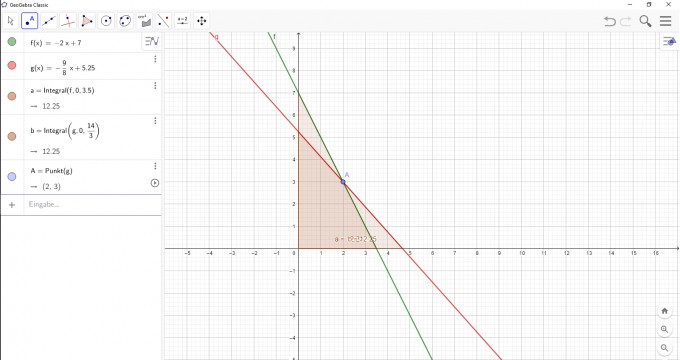
Deine lineare Funktion schließt mit den Koordinatenachsen eine Fläche ein (ein rechtwinkliges Dreieck mit einer Höhe von h=f(0)=n und einer weiteren Kathete mit der Länge l=x0).
Demzufolge:
$$A=\frac{1}{2}*h*l=\frac{1}{2}*n*x_0=\frac{1}{2}*n*(-\frac{2n}{3-n})=\frac{49}{4}$$
$$\frac{49}{2}=n*(-\frac{2n}{3-n})=-\frac{2n^2}{3-n}$$
$$\frac{147}{2}-\frac{49}{2}n=-2n^2$$
$$0=-2n^2+\frac{49}{2}n-\frac{147}{2}$$
$$0=n^2-\frac{49}{4}n+\frac{147}{4}$$
$$n_{1,2}=\frac{49}{8}±\sqrt{\frac{2401}{64}-\frac{147}{4}}$$
$$n_{1,2}=\frac{49}{8}±\frac{7}{8}$$
$$n_1=7$$
$$n_2=\frac{21}{4}$$
Einsetzen in die Gleichung für m:
$$m_1=\frac{3-n_1}{2}=\frac{3-7}{2}=-2$$
$$m_2=\frac{3-n_2}{2}=\frac{3-5,25}{2}=-\frac{9}{8}$$
Somit ergeben sich die Gleichungen:
$$f_1(x)=-2x+7$$
$$f_2(x)=-\frac{9}{8}x+5,25$$