Schnittpunkt der Geraden senkrecht zu g durch P und der Mittelsenkrechten von A und P.
2/9·(x - 6) + 3 = - (x - 8) + 5
x = 102/11 = 9.273
y = 2/9·((102/11) - 6) + 3 = 41/11 = 3.727
M = [102/11, 41/11]
Abstand
|MA| = √((102/11 - 10)^2 + (41/11 - 7)^2) = √(1360/121)
Kreisgleichung
(x - 102/11)^2 + (y - 41/11)^2 = 1360/121
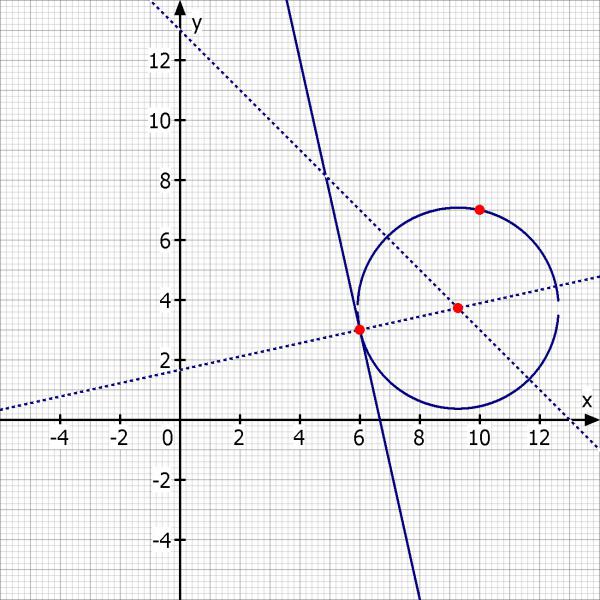
Skizze: