Deine Gleichung stimmt, nützt dir aber wahrscheinlich nichts. Wenn du nur theoretisch mit Formeln den Induktionsbeweis führst, heißt das noch nicht, dass die Überdeckung auch gelingt.
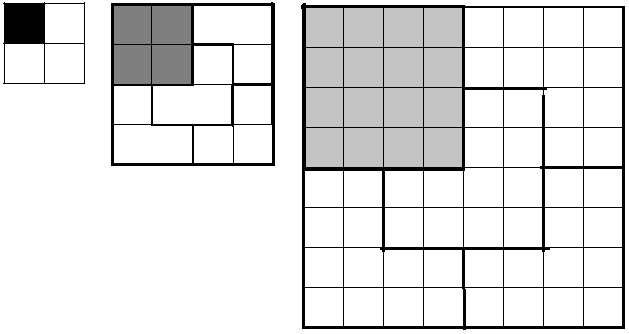
Beginne zeichnerisch mit einem 2×2-Feld und überlege dann, wie man ein 4×4-Feld überdecken könnte, in dem ein 2×2-Feld bereits bedeckt ist. Dann bekommst du vielleicht eine Beweisidee.
Hier eine Anregung: