Aufsuchen eines Graphen
Gegeben ist die Formel \( p = (3·q·r^2) / s \) mit \( p, q, r, s \in ℝ^{+} \). Aus dieser Formel können verschiedene funktionale Zusammenhänge herausgelesen werden.
Welcher der abgebildeten Funktionsgraphen passt jeweils zu folgendem funktionalen Zusammenhang?
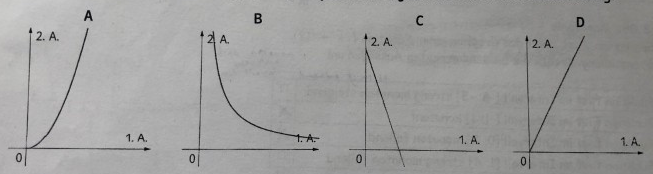
\( \begin{array}{ll}{ p = f(q), \text { wobei } r \text { und } s \text { konstant sind: }} & {\text { Graph: } D} \\ { q =g(r), \text { wobei } p \text { und } q \text { konstant sind: }} & {\text { Graph: } A} \\ { p =h(s), \text { wobei } r \text { und } q \text { konstant sind: }} & {\text { Graph: } B} \end{array} \)
Kann mir jemand bitte das Beispiel erklären. Wie weiß man wie sich der Graph verändert, wenn man p,q,r,s verändert?