Wie ist das Rotationsvolumen diese Ei und wie berechne ich die Aufgabe?

Question

Aufgabe:

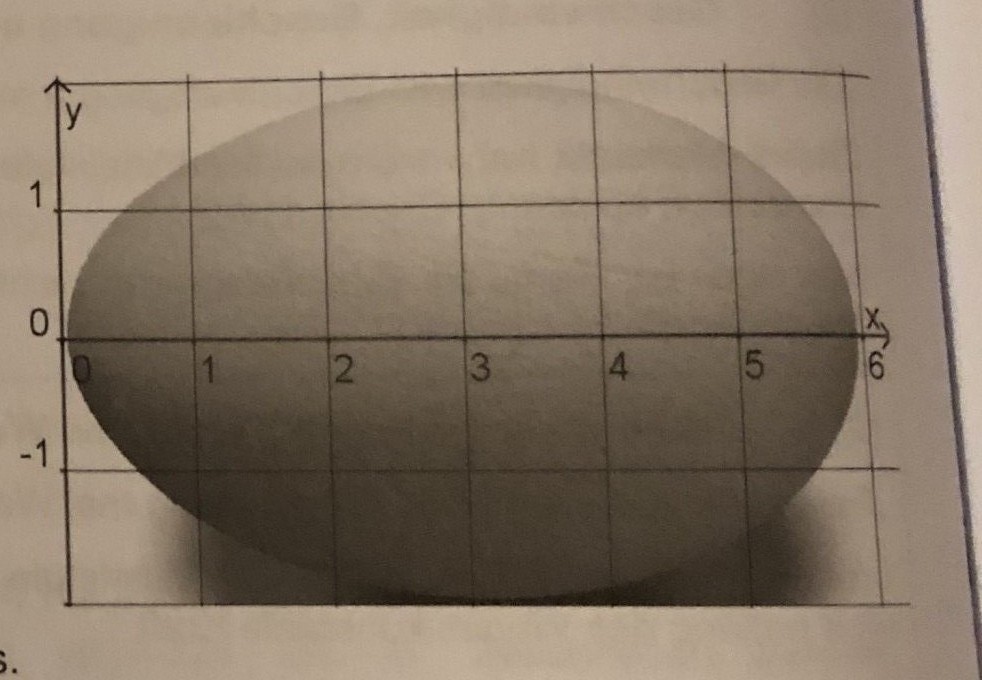
In erster Näherung ist das Ei ellipsenförmig. Eine ellipse lässt sich beschreiben durch folgende funktionsgleichung:

f(x)= a*Wuzel aus 1-(x-b)^2/b^2

Begründen sie am Therm und anhand der Abbildung, dass a≈2 und n≈3 als erste Näherungswerte geeignet sind.

Passen sie durch Experimentieren die Parameter dem Verlauf an.

Erarbeiten sie eine Strategie zur Berechnung des Eivolumen.

Problem/Ansatz:

Ich weiß wie man ein Rotationvolumen berechnet. Diese Aufgabe verstehe ich dennoch nicht.

Comments

a und b sind die Halbachsen der Ellipse, also die Hälfte der Breite und die Hälfte der Höhe des Ei. Beide Größen kannst du in dem Bild ablesen.

---

Und wie passe ich die Parameter an?

---

a=2 und b=3 sind nur Näherungswerte, wenn man im Bild die Längen misst sind die echten Werte sicher etwas kleiner. Probier mal a=1.9 und b=5.95

Vergleiche mit a=2 und b=3 un entscheide, was besser die Form wiedergibt.

Answer 1

Setze doch a=2 und b=3 in den Term ein.

Und dann berechne f(0)=2*√(1-9/9)=0 und der Punkt (0;0) passt doch.

Berechne entsprechend f(3) und f(6) und vergleiche mit dem Bild.