Übergangswahrscheinlichkeiten durch zwei Zustände

Question

Ein bestimmtes System lässt sich durch zwei wohldefinierte Zustände beschreiben: Zustand 1 und Zustand 2. In regelmäßigen Zeitabständen kann das System seinen Zustand zufällig wechseln, und zwar nach folgenden Regeln: Befindet sich das System in Zustand 1, so wechselt es zu Zustand 2 mit 50%-ger Wahrscheinlichkeit; befindet sich das System in Zustand 2, so wechselt es zu Zustand 1 mit 25%-ger Wahrscheinlichkeit. Diese Übergangswahrscheinlichkeiten können wir graphisch wie folgt darstellen:

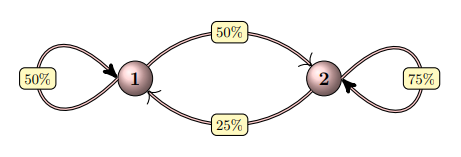
Benutzen Sie das Ergebnis [ \( C^{n}=\frac{1}{3}\left(\begin{array}{ll}{4^{n}+2} & {2\left(4^{n}-1\right)} \\ {4^{n}-1} & {2 \cdot 4^{n}+1}\end{array}\right) \) ], um folgende Frage zu beantworten:

Wenn man das System über beliebig lange Zeitspannen beobachtet, mit welcher Wahrscheinlichkeit befindet es sich in Zustand 1 bzw. in Zustand 2?

Ich bin mir irgendwie total unschlüssig, wie ich an die Sache heran gehen soll. Wäre cool, wenn mir jemand helfen könnte :)

Comments

Die Auswertung des Übergangsgraphen ergibt die Wahrscheinlichkeiten 1/3 und 2/3. Woher stammt die Matrix C^n und was steht sonst noch in der Aufgabe?

Answer 1

Die Übergangsmatrix ist B := \(\begin{pmatrix} \frac{1}{2}&\frac{1}{4}\\\frac{1}{2}&\frac{3}{4} \end{pmatrix}\).

Bestimme B^∞ := lim_n→∞ Bⁿ.

Bestimme damit B^∞ · v mit einem beliebigen zweizeiligen Vektor v.

Die Wahrscheinlichkeit, sich im ersten Zustand zu befindet, nähert sich mit wachsendem n beliebig nahe der ersten Komponente des Ergebnisses an.

Die Wahrscheinlichkeit, sich im zweiten Zustand zu befindet, nähert sich mit wachsendem n beliebig nahe der zweiten Komponente des Ergebnisses an.