Katheten- und Höhensatz anwenden; Mathebuch Formel M10

Question

Aufgabe:

Die Schüler Andrea(A), Bernd(B), Claudia(C) und Daniel(D) möchten mithilfe des Stadtplanes berechnen, wie weit ihre Wohnungen voneinander entfernt liegen (Luftlinie).

Sie zeichnen die Verbindungslinien ein.

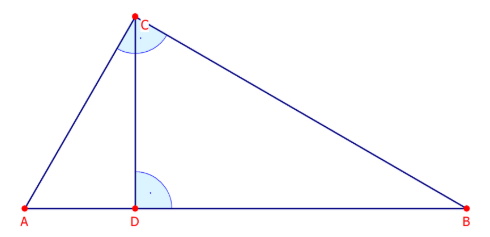
Sie wissen bereits das die Strecke AC doppelt so lang ist wie die Strecke AD und dass Daniel von Bernd 9 km entfernt wohnt.

Berechne die Länge der Strecken AB, AC, AD, BC und CD

Problem/Ansatz:

Ich komm leider bei dieser Mathe Aufgabe nicht weiter. Meine Mittschüler können mir leider auch nicht helfen und im Internet steht auch nichts brauchbares. Unser Mathe Lehrer ist derzeit krank und konnte ihn auch nicht fragen. Wir haben das Thema Katheten- und Höhensatz erst angefangen. Konnte leider auch keine Skizze vom Buch hinzufügen.

ich würde mich freuen wenn mir jemand weiterhelfen könnte und mir den Rechenweg erklären kann. Bin echt ratlos und weiß nicht mehr weiter.

Answer 1

Ich beschreib euch die Skizze

                            C

                              |

                      h    |

                              |

A_______________|______________________B

          p                   D         q=9km

Falls ich D richtig eingezeichnet habe (?).

Bitte stellt euch noch vor das AC und BC verbunden sind

Und bei C ist ein rechter winkel

Sie wissen bereits das die Strecke AC doppelt so lang ist wie die Strecke AD und dass Daniel von Bernd 9 km entfernt wohnt. AC = 2p

Zudem (kürzere Kathete : Hypotenuse) = 1 : 1 in allen drei "ähnlichen Dreiecken" in deiner Skizze. 

Höhensatz: pq = h^2

Was folgt nun?

[spoiler]

z.B.

1 : 2 = AC : AB

1 : 2 = 2p : (p + q)

1 : 2 = 2p : (p + 9)    Lässt sich nach p auflösen. Danach ist der Rest nicht mehr schwierig.

Comments

Ja D ist richtig

Hab es voher vergessen Sry

Answer 2

 AD = q
AC = 2q
BD = 9 km

Mit dem Kathetensatz gilt:
q·(q + 9) = (2·q)^2
q^2 + 9·q = 4·q^2
3·q^2 - 9·q = 0 → q = 3 km (∨ q = 0)

Damit ergeben sich:
AB = p + q = 12 km
AC = 2·q = 6 km
AD = q = 3 km
BC = √(9^2 + √27^2) = √108 = 10.392 km
CD = √(p·q) = √27 = 5.196 km

Answer 3

Kathetensatz

(2p)^2 = p*(p+9)

<=>  4p^2 = p^2 + 9p

<=> 3p^2 = 9p

und weil p>0 also  3p=9  bzw  p=3 .

Dann  Höhensatz    h^2 = p*q ==>   h^2 = 3*9 = 27 ==>  h = √27

Andere Kathete

a^2 = 9*(3+9) = 9*12 = 108

==>  a = √108

Probe mit Pythagoras:  36 + 108 = 144 OK

Comments

Danke an alle für eure Hilfe aber ich hab noch eine frage wie kommt man auf die 3q?