hi
a)
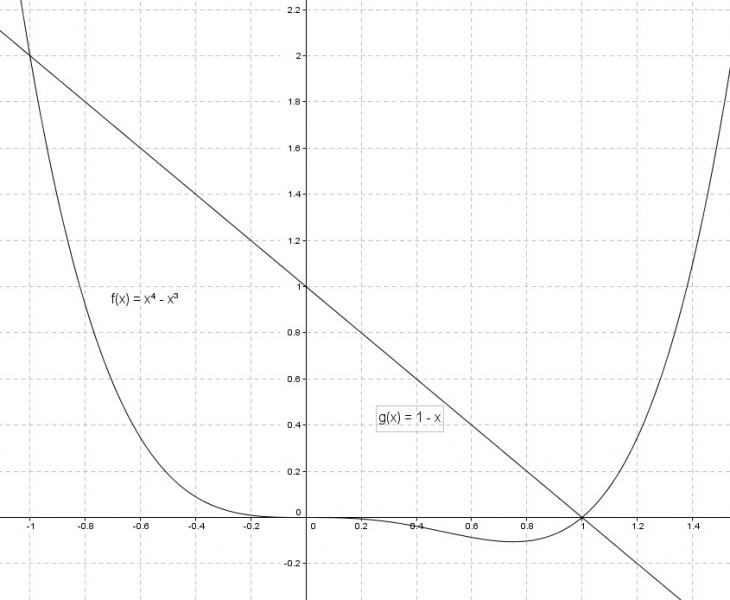
schnittstellen bestimmen
x^4 - x^3 = 1 - x
x^4 + x - x^3 -1 = 0
x1 = 1, x2 = -1
die graphen schneiden sich an der stelle
x1 = 1 und x2 = -1
fläche unter g(x) von -1 bis 1
A1 = ∫1 - x dx = [-x^2/2 + x](von -1 bis 1) = 2
fläche unter f(x) von -1 bis 0
A2 = ∫x^4 - x^3 dx = [x^5/5 - x^4/4](von -1 bis 0) = 9/20
fläche unter f(x) von 0 bis 1
A3 = ∫x^4 - x^3 dx = [x^5/5 - x^4/4](von -1 bis 0) = -1/20
fläche zwischen den graphen
A = A1 - A2 + |A3|
A = 2 - 9/20 + |-1/20|
A = 7/5
b)
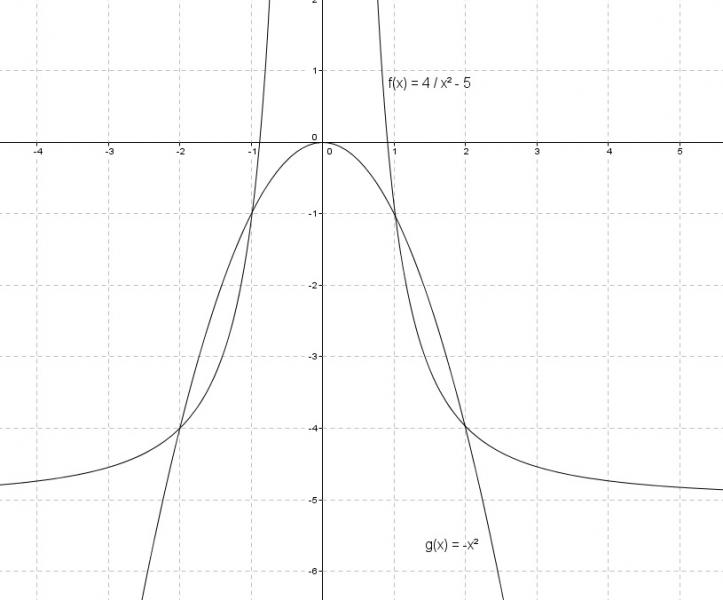
schnittstellen bestimmen
4/x^2 - 5 = -x^2
x^4 - 5x^2 + 4 = 0
x^2 = z
z1,2= 2.5 ± √(6.25-4)
z1 = 4, z2 = 1
x = ±√z
x1,2 = ±2
x3,4 = ±1
die graphen schneiden sich an der stelle
x1 = 2, x2 = -2, x3 = 1, x4 = -1
fläche unter f(x) von 1 bis 2
A1 = ∫4/x^2 - 5 = [-4/x - 5x](von 1 bis 2)
A1 = -3
fläche unter g(x) von 1 bis 2
A2 = ∫-x^2 dx = [-x^3/3](von 1 bis 2)
A2 = -7/3
fläche zwischen den graphen, nutzung der symmetrie
A = 2(|A1| - |A2|) = 2(|3|-|7/3|)
A = 4/3