Voraussetzung: A und B sind Punkte auf einem Kreis. Die Tangenten in den Punkten A und B sind parallel.
Behauptung: Die Strecke AB ist ein Durchmesser.
Versuch eines Beweises:
Es muss gezeigt werden, dass der Kreismittelpunkt M auf der Strecke AB liegt.
Nehmen wir einmal an, M läge nicht auf der Strecke AB. Dann bilden die Punkte MAB ein Dreieck.
(In der Abbildung sind die Bezeichnungen etwas anders.)
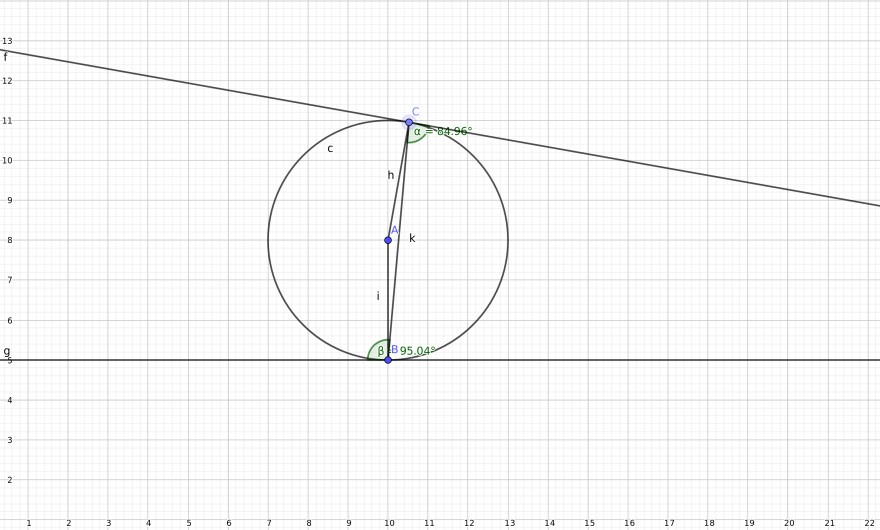
Die Winkel α und β wären unterschiedlich groß, müssen aber als Wechselwinkel an Parallelen gleich groß sein. Daher muss M auf AB liegen und die Strecke von A nach B ist ein Durchmesser.
(Ob die Gegenrichtung auch gezeigt werden muss, geht aus der Fragestellung nicht genau hervor.)