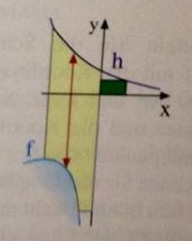
Aufgabe Küstenstraße:
Gegeben ist die Funktion \( f(x)=\frac{2}{x} \cdot e^{-x+1} \) Teil I
a) Weisen Sie nach, dass der Graph von \( \mathrm{f} \) die Koordinatenachsen nicht schneidet.
b) Bestimmen Sie den Punkt \( \mathrm{P} \), in dem die Tangente an \( \mathrm{f} \) waagerecht verläuft.
c) Sei \( \mathrm{h}(\mathrm{x})=\mathrm{x} \cdot \mathrm{f}(\mathrm{x}) . \) Zeichnen Sie den Graphen von \( \mathrm{h} \) für \( -1 \leq \mathrm{x} \leq 4 \).
d) Wie muss \( \mathrm{u}>0 \) gewählt werden, damit das Rechteck \( \mathrm{O}(0 \mid 0), \mathrm{A}(\mathrm{u} / 0), \mathrm{B}(\mathrm{u} \mid \mathrm{h}(\mathrm{u})) \) und
\( \mathrm{C}(0 \mid \mathrm{h}(\mathrm{u})) \) möglichst geringen Umfang hat?