Schattenbilder im Koordinatenraum konstruieren

Question

Aufgabe:

Im Koordinatenraum steht ein schräg nach oben geneigtes Dreieck ABC mit A(3/2/0) B(3/6/0) und C(2/3/4).

In Richtung des Vektors (-1/-3/-1) fällt paralleles Licht auf dieses Dreieck.

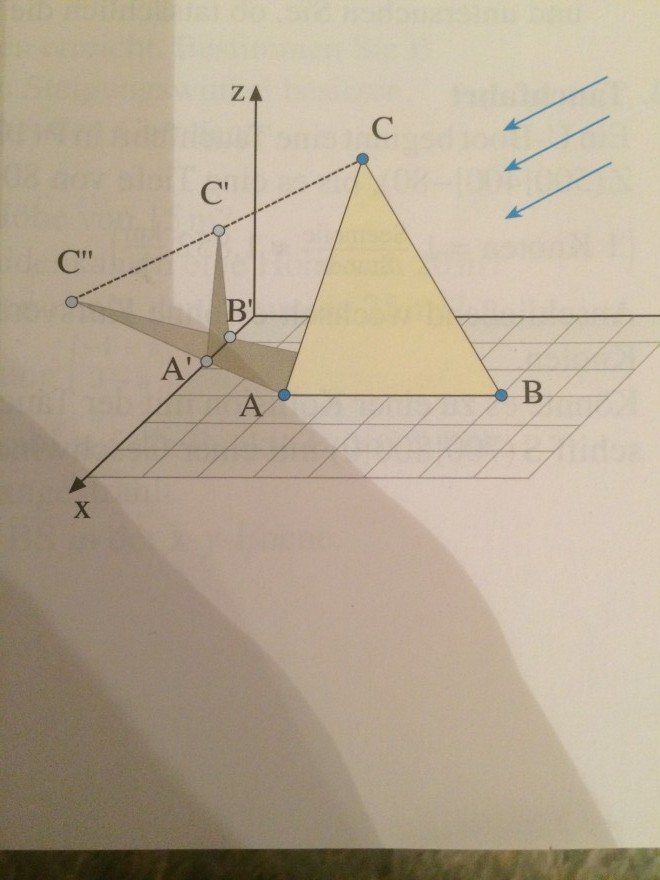
Zeichne das Schattenbild des Dreiecls, wobei sie sich an der (nicht maßstäblichen) Skizze orientieren. Berechnen Sie dann die Exkpunkte des Dreiecksschattens auf dem Boden und den Wänden des Raums.

Wie kann ich die Punkte A‘ und B‘ berechnen?

Text erkannt:

11
$$ \begin{array}{c} {\text { u }} \\ {\text { N- } u \text { b } \frac{\pi}{2} \text { is }} \\ {=\sqrt{2}} \end{array} $$

Answer 1

Man soll sich vorstellen, dass die xz-Ebene eine Wand ist, und dass das Dreieck A'B'C' ein Teil des Schattens ist. Der Punkt C' ist derjenige Punkt mit der zweiten Koordinate 0, der auf der Geraden durch C mit dem Richtungsvektor v (dem gegebenen Vektor der Sonnenstrahlen) liegt. An der Skizze soll man sich vermutlich klar machen, dass C" ebenfalls auf dieser Geraden liegt und die dritte Koordinate 0 hat. Dieser Punkt ist der äußerste Punkt des Schattens auf dem "Boden", wenn die Wand (die xz-Ebene) "entfernt" wird. Die Punkte A' bzw. C' sind nun die Punkte auf der x-Achse (also zweite und dritte Koordinate 0), die auf den Geraden durch C'' und A bzw. B liegen.