Kostenfunktion: Gewinnschwelle und Gewinngrenze bestimmen

Question

Kann mir einer Helfen ein paar Aufgaben zu lösen?

Aufgabe 3: Gegeben ist die Erlösfunktion E (x) = 20 * x und die Kostenfunktion K (x) = x³ - 10 * x² + 35 * x + 18.

a:Bestimme die Gewinnschwelle und die Gewinngrenze! b:Bestimme das Gewinnmaximum! Welcher Gewinn wird hier erzielt? c: Welche Kosten treten an der Gewinnschwelle und an der Gewinngrenze auf? d: Skizziere die Gewinnfunktion, markiere die Gewinntine und das Gewinnmaximum!

Ich hoffe einer kann mir hier Helfen, ich wäre sehr dankbar dafür.

LG

Answer 1

G(x) = E(x) - K(x) = 20·x - (x^3 - 10·x^2 + 35·x + 18) = - x^3 + 10·x^2 - 15·x - 18

a:Bestimme die Gewinnschwelle und die Gewinngrenze!

Das sind hier die Nullstellen

G(x) = 0
x = 7.772001872 ∨ x = -0.7720018726 ∨ x = 3

Gewinnschwelle = 3
Gewinngrenze = 7.772

b: Bestimme das Gewinnmaximum! Welcher Gewinn wird hier erzielt?

Maximum G'(x) = 0
- 3·x^2 + 20·x - 15 = 0
x = 0.8612671709 ∨ x = 5.805399495

Gewinnmaximum bei x = 5.805399495

Maximaler Gewinn G(5.805) = 36.28821605

c: Welche Kosten treten an der Gewinnschwelle und an der Gewinngrenze auf?

K(3) = ...
K(7.772) = ...

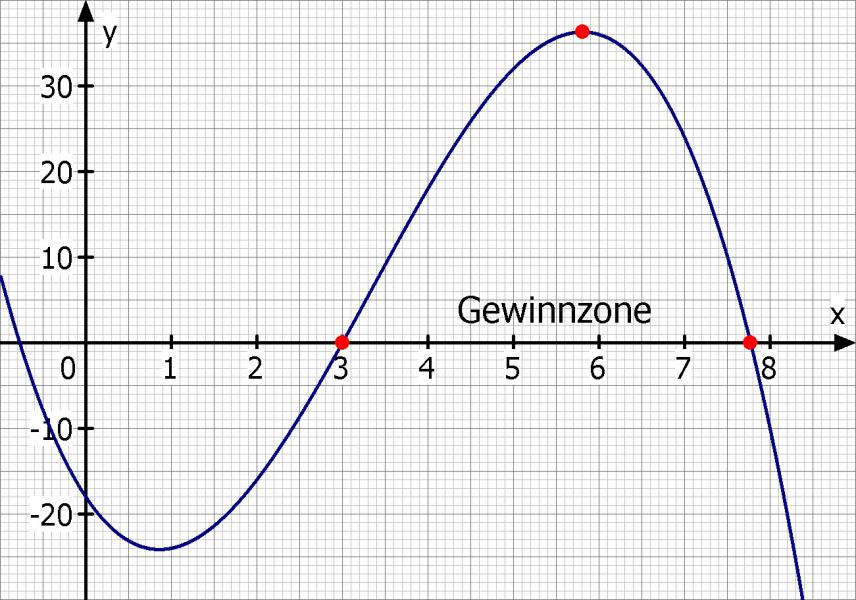
d: Skizziere die Gewinnfunktion, markiere die Gewinnzone und das Gewinnmaximum!

Comments

gewinnschwelle und grenze wie hast du die gewinnfunktion 0 gesetzt und 3 und 7 raus bekommen ??

---

Du kennst eine Nullstelle bei 3 und machst damit eine Polynomdivision. Dann hast du eine quaratische Gleichung und bestimmtst noch die anderen 2 Nullstellen.

---

entschuldige die ebt blöde frage aber woher kenne ich denn die 3 als nullstelle ?

---

Wenn du deine Funktion ansiehst, muss die Nullstelle ein Teiler von 18 sein, damit das in der Schule als Beispiel vorkommen kann.

Du musst also ±1, ±3, ±2, ±6, ±9 und ±18 testen.

---

Vielen Dank für die Ausführliche Erklärung des Lösungsweges.

Ich habe es ohne Probleme nachvollziehen können.

Nochmals vielen Dank

Ich werde es in der Klausur 1 zu 1 anwenden und hoffe daher eine 1.0 zu bekommen.

Ich hoffe ihr vorgegebener Rechenweg wird vom Dozenten anerkannt und mit voller Punktzahl bewertet.