Verstehe die Ableitung nach theta beim Summenzeichen nicht

Question

lx(Θ)= n log (2) - n/2 log(√2πθ) - ∑(xi²/2πθ)

->ableiten

l´x(Θ)= -n/2 * 1/2πθ * 2π - 1/2 + (-1/θ²) ∑xi²  (Ableitung aus Musterlösung)

Kann das einer nachvollziehen und in einzelnen Schritten erklären?

EDIT(Lu): Achtung: Foto unabdingbar in der Fragestellung und im erkannten Text fehlen zu viele Klammern usw. 
(Siehe Foto)

Text erkannt:

\( \ell_{x}(6)=4 \log (2)-\frac{4}{2} \cdot \lg (2 \pi \theta)-\sum \limits_{i=1}^{n} \frac{x_{2} R}{2 \theta} \)
\( \ln (\theta)=\frac{n}{2} \frac{1}{\pi \theta} \cdot 2 \pi-\frac{1}{2} \cdot\left(-\frac{1}{\theta^{2}}\right) \sum \limits_{i=1}^{n} t_{2}^{2} \)
\( \quad=-\frac{n}{2 \theta}+\frac{1}{20^{2}} \sum \limits_{i=1}^{2} x^{2}=0 \)

Liebe Grüße,

Comments

Vom Duplikat:

Titel: Ableitung nach theta mit Summenzeichen: Umformung unklar

Stichworte: termumformung,ableitung,theta,summenzeichen

Aufgabe:

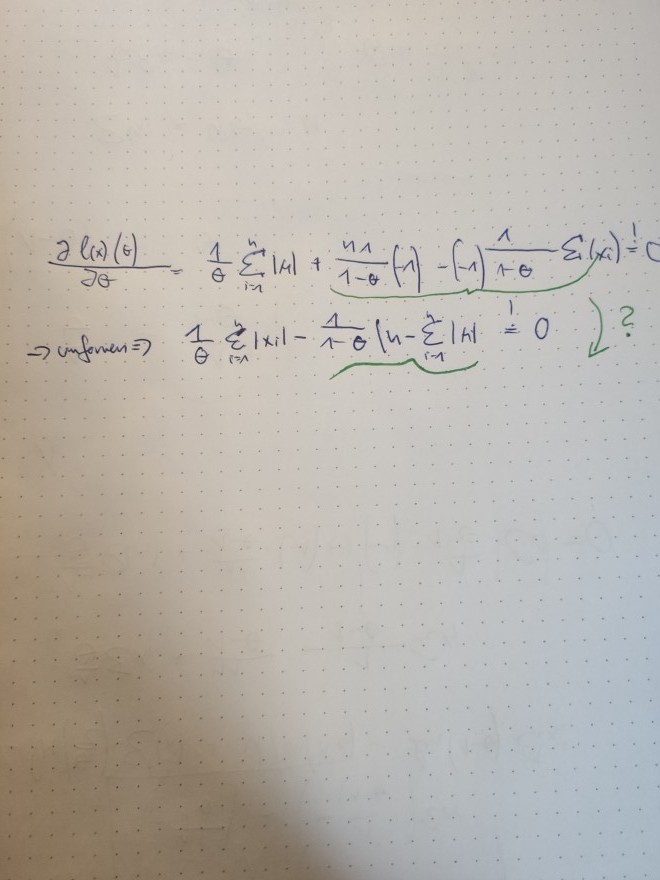
Text erkannt:

\( \begin{array}{|c|c|}\hline 0 & {0} \\ \hline x & {y} \\ \hline x & {0} \\ \hline y & {-x} \\ \hline x & {y} \\ \hline x & {y z} \\ \hline x & {y} \\ \hline 5 & {y} & {y} \\ \hline\end{array} \)
\( =\frac{\frac{5}{2}}{40} \cdot \frac{\frac{1}{7}}{50} \)
$$ \sum \limits_{r=1}^{r} \frac{\sqrt{n}}{r} $$

Ich verstehe die Umformung nicht..kann mir das jemand erklären?

Lg

---

Also nur das Foto beachten. Keine Ahnung was da das Programm noch eingefügt hat.

---

Von Fehlpost mit fehlendem Bild.

Titel: Verstehe folgende Ableitung nicht

Stichworte: ableitung

lx(Θ)= n log (2) - n/2 log(√2πθ) - ∑(xi²/2πθ)

->ableiten

l´x(Θ)= -n/2 * 1/2πθ * 2π - 1/2 + (-1/θ²) ∑xi²   (Ableitung aus Musterlösung)

Kann das einer nachvollziehen und in einzelnen Schritten erklären?

Liebe Grüße,

Stefan

---

Die Musterlösung sieht sicher nicht so aus. Setze Klammern, wo sie hingehören (oder schicke eine Abbildung der Musterlösung).

---

Siehe neuen Frage. Da habe ich das Foto eingefügt ;)

---

Ist deine Frage inzwischen dank https://www.mathelounge.de/694143/verstehe-die-ableitung-nicht beantwortet?

@mathelounge: Zimbasa hat auf deine Meldung reagiert. Daher Frage wieder einblendet. Bitte mit einem Kommentar auf den Kommentar von Zimbasa reagieren.

Rechenschritt:

Erst mal wurden die beiden (-1) vorgezogen und aus dem PLUS ein MINUS.

Analog zu:

3 + 3(-1) + 78(-1)

= 3 - (3 + 78)

Dann wurde auch noch 1/(1 Minus Theta) ausgeklammert, analog zu

3 - (3 + 78)

= 3 - 3 ( 1 + 78/3 )

= 3 - 3 ( 1 + 26 )

Wenn ich mich nicht verrechnet habe.

---

Bitte Formeln eingeben, sodass man sie lesen kann.

Hierzu das Latex-Tool verwenden: https://www.matheretter.de/rechner/latex

1. Frage bearbeiten

2. Formeln einfügen

3. Bild löschen

Danke.

Answer 1

Bei welchem Summanden hast du denn Schwierigkeiten beim Ableiten?

Konstante Summanden werden zu 0 abgeleitet.

Faktoren bleiben in der Ableitung erhalten.

Potenzen werden mit der Potenzregel abgeleitet.

Der natürliche Logarithmus wird bei dir mittels Kettenregel abgeleitet wobei die Ableitung von LN(x) einfach 1/x ist.