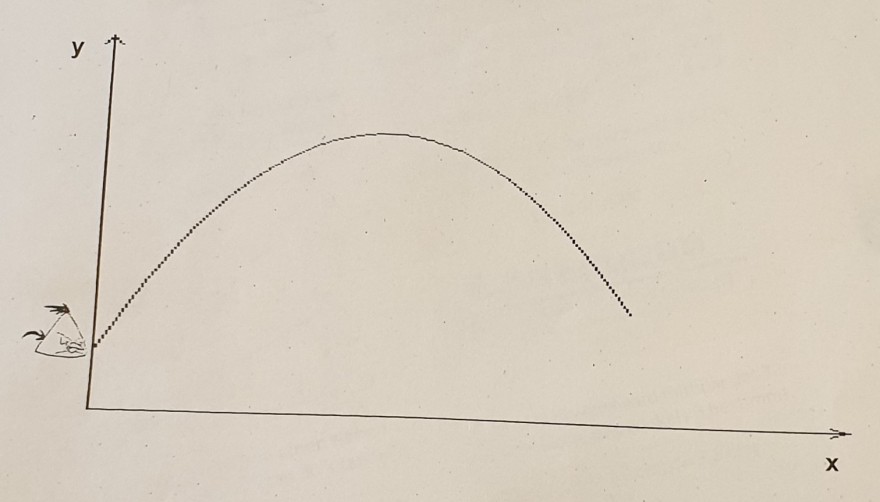
In dem Computerspiel ,,Angry Birds" werden virtuelle Vögel auf verschiedene Ziele geschossen. Die Flugbahnen der Vögel sind Graphen von quadratischen Funktionen. Die Flugbahn eines Vogels lässt sich durch die folgende Gleichung beschreiben:
y=-x^{2}+8x+4
x entspricht der horizontalen Entfernung des Vogels zum Abschussort in m,
y entspricht der aktuellen Höhe des Vogels über dem Erdboden in m.
Text erkannt:
a) Berechne, aus welcher Höhe der Abschuss des Vogels erfolgt.Schnittpankt berechnen: \( y=-x^{2}+8 x+4 \)
\( \Rightarrow y=-x^{2}+8 x+4 \)
\( \Rightarrow x=0 \)
\( y=-0^{2}+8 \cdot 0+4=4 \)
\( y=4 \)
\( H=4 \)
b) Berechne, in welcher Höhe sich der Vogel nach 6 m (x=6) Flug befindet.
x=6
\( y=-6^2+8 \cdot 6+4=16 \)
\( y=16 \)
\( H=16 \)
c) Berechne, ob der Vogel ein Ziel treffen würde, das sich 8 m (x=8) entfernt in einer Höhe von 3 m befindet.
\( y=-8^{2}+8 \cdot 8+4=4 \)
nein der Vogel würde kein Ziel treffen denn \( 3 \neq 4 \)
d) Nach wie vielen Metern kommt der Vogel auf den Boden, wenn kein. Hindernis im Weg ist?
Y=-x^2+8x+4
4= -x^2+8x+4 /-4
0= -x^2+8x
0= x^2-8x
Pq-Formel anwenden: x1=0 und X2=8
X2-X1 = 8-0 = 8
Nach 8 m kommt der Vogel auf den Boden
e) Welche maximale Höhe erreicht der Vogel während des Fluges?
-(p/2) in Funktion einsetzen:
-(p/2)=8/2 = 4
also 4 in Funktion einsetzen:
Y = -4^2+8*4+4 = 20m
Habe ich die Aufgaben richtig berechnet?