Hallo Leni,
mach Dir zunächst eine Skizze. So wie diese hier
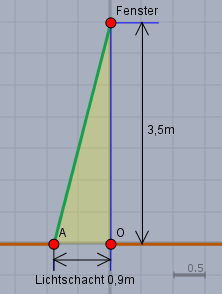
\(AF\) (grün) sei die Leiter. Die Strecke \(AO\) ist der Lichtschacht vor der Hauswand. Bis zum Fenster \(F\) sind es 3,5m. Dort sieht man ein rechtwinkliges Dreieck \(\triangle OAF\). Und da Ihr den Satz des Pythagoras gelernt habt, ist dann$$\begin{aligned} |AF|^2 &= |AO|^2 + |OF|^2 \\ &= 0,9^2 + 3,5^2 \\& = 13,06 \\ \implies |AF| &= \sqrt{13,06} \approx 3,61 \end{aligned}$$D.h. die Leiter sollte mindestens 3,61m lang sein, damit sie bis zum Fenster reicht.
Ist nur eine 3,5m lange Leiter vorhanden, so kannst Du genauso ausrechnen wie hoch diese reicht. Angenommen der höchte Punkt der Leiter sei \(F'\) so ist $$\begin{aligned}|AF'|^2 &= |AO|^2 + |OF'|^2 \\ \implies |OF'|^2 &= |AF'|^2 - |AO|^2 \\&= 3,5^2 - 0,9^2 \\&=11,44 \\ \implies |OF'| &= \sqrt{11,44} \approx 3,38\\ \end{aligned}$$die 3,5m lange Leiter reicht also auch 3,38m hoch bis kurz unter das Fenster.
Gruß Werner