Brauche Hilfe bei Trigonometrie

Question

Könnte mir bitte jemand bei dieser Übung die Lösung sagen, mir einem Rechnungsweg bitte. Es wäre nett, wenn jemand sich damit auskennt und mit helfen würde.

Flugrichtung 1

Geschwindigkeiten stellt man in der Physik durch Pfeile dar, Geschwindigkeiten mit verschiedenen Richtungen setzt man zusammen, indem man aus den Geschwindigkeitspfeilen Dreiecke bildet.

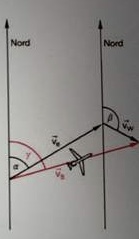
Im nebenstehenden Bild wird die Eigengeschwindigkeit des Flugzeugs \( \vec{v}_{c} \) und die Windgeschwindigkeit \( \vec{v}_{w} \) zur Geschwindigkeit \( \vec{v}_a \) überlagert, die die Bewegung des Flugzeugs über dem Boden angibt. \( \alpha \) ist der "Kompasskurs", \( \beta \) die Windrichtung und \( \gamma \) die Flugrichtung.

Ein Flugkapitän steuert den Kompasskurs \( 75^{\circ} \), das Flugzeug hat die Eigengeschwindigkeit \( 250 \mathrm{km} / \mathrm{h} \). Der Wind weht aus Nord-West mit der Geschwindigkeit \( 50 \mathrm{km} / \mathrm{h} \).

Tipp: Steuert ein Flugzeug den Kurs \( 0^{\circ} \), so fliegt es genau Richtung Norden, bei einem Kurs von \( 90^{\circ} \) genau Richtung Osten, bei einem Kurs von \( 180^{\circ} \) genau Richtung Süden und bei einem Kurs von \( 270^{\circ} \) genau Richtung Westen.

Bestimme die Flugrichtumg des Flugzeugs und die Geschwindigkeit des Flugzeugs über dem Boden.

Answer 1

Die West-Ost-Komponente (x-Achse) von v_c ist 250 km/h * sin 75° und diejenige von v_w ist 50 km/h * sin 45° also addiert 276,8368 km/h.

Die Süd-Nord-Komponente (y-Achse) von v_c ist 250 km/h * cos 75° und diejenige von v_w ist - 50 km/h * cos 45° also addiert 29,3494 km/h.

Die Geschwindigkeit über Grund ergibt sich mit Pythagoras als 278,4 km/h und der Azimut als arctan(276,8368 / 29,3494) ≈ 84°.

Answer 2

Das Flugzeug hat eine Geschwindigkeit von ungefähr 278,4 km/h (Kosinussatz).

Answer 3

Hallo Aaron1778,

hier kannst du ganz normale Berechnungen in einem Dreieck machen. Zuerst wendest du den Kosinussatz an:

allgemein: \( c^{2} \) =\( a^{2} \) +\( b^{2} \) -2ab*cos(γ )

bei dieser Aufgabe:

\(c=\sqrt{vc^{2}+vw^{2}-2*vc*vw*cos(α+180°-β)} \)

\(c=\sqrt{250\frac{km}{h}^{2}+50\frac{km}{h}^{2}-2*250\frac{km}{h}*50\frac{km}{h}*cos(75°+180°-135°)} \)

c=278,388\( \frac{km}{h}=va \)

Und für den Winkel kannst du dann einfach den Sinussatz nehmen:

allgemein: \( \frac{a}{sin(α)}=\frac{b}{sin(β)} \)

bei dieser Aufgabe:

\( \frac{vw}{sin(γ-α)}=\frac{va}{sin(α+180°-β)} \)

\(sin(γ-α)=\frac{vw*sin(α+180°-β)}{va}\)

\(sin(γ-α)=\frac{50\frac{km}{h}*sin(75°+180°-135°)}{278,388\frac{km}{h}}\)

\(sin(γ-α)=0,1555\)

γ-α=8,948°

γ=83,948°