Aufgabe:
Aufgabe 8 (Teil B)
Brücken zwischen Gebäuden
Gebäude können durch Brücken verbunden werden.
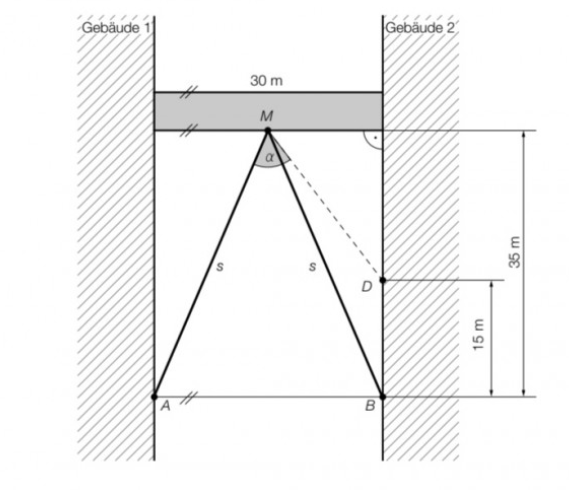
a) Eine \( 30 \mathrm{m} \) lange Brücke wird im Punkt \( M \) auf zwei Stützen der Länge s gelagert (siehe obenstehende Abbildung).
1) Berechnen Sie die Länge \( s \) einer Stütze.
Die Stütze \( M B \) soll durch eine neue Stütze \( M D \) ersetzt werden.
2) Berechnen Sie den Winkel \( \alpha \).
Problem/Ansatz:
Ich bräuchte nur bei B) Hilfe. Ich weiß nicht wie man bei AD auf 15^2+30^2 kommt, Ich dachte eher an 30^2+20^2 Biitee um Hilfe,
Lösung
a2) Ansatz: \( \overline{A D^{2}}=s^{2}+\overline{M D^{2}}-2 \cdot s \cdot \overline{M D} \cdot \cos (\alpha) \)
\( \overline{A D}=\sqrt{15^{2}+30^{2}}=\sqrt{1125} \)
\( \overline{M D}=\sqrt{20^{2}+15^{2}}=\sqrt{625}=25 \)
\( 1125=1450+625-2 \cdot \sqrt{1450} \cdot 25 \cdot \cos (\alpha) \Rightarrow \alpha=60,06 \ldots^{\circ} \)
Der Winkel beträgt rund \( 60,1^{\circ} \).