Wie Integral mit Betrag berechnen?

Question

Aufgabe:

Es sei g(x)= 3|x^2 - 1|

Bestimme das Integral in Abhängigkeit von t ist größer gleich 0 ( Integral geht on -1 bis t )

Wie berechnet man das Integral?

Answer 1

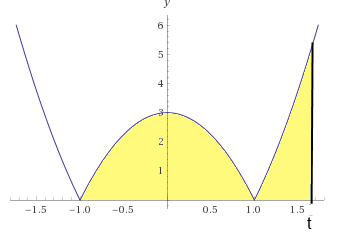
Die Nst. sind -1 und 1.

Im Bereich [-1,1] ist die Kurve eine nach unten geöffnete Parabel, also wenn t≤1 ist, musst du -3(x²-1) von -1 bis t integrieren.

Wenn t>1 ist musst du in 2 Abschnitten integrieren: du integrierst wie gerade beschrieben von -1 bis 1 und addierst dieses Ergebnis zu dem Integral von 1 bis t von +3(x²-1).

falls t≤1: A=\( \int\limits_{-1}^{t} \) (-3(x²-1)) dx

falls t>1: A=\( \int\limits_{-1}^{1} \) (-3(x²-1)) dx + \( \int\limits_{1}^{t} \) 3(x²-1) dx

Comments

Dankeschön:)