Anlässlich des Pi-Days \(2020\) melde ich mich mit einem kleinen Artikel zu \(\pi\). Ich erkläre ich dir, wie du mithilfe eines Pseudozufallszahlengenerators die Kreiszahl \(\pi\) berechnen kannst.
1. Einführung
Wie kann man den Zufall dazu nutzen, um die Kreiszahl \(\pi\) zu berechnen? Das ist eine Frage, die Bewerber schon in Coding-Interviews gestellt bekommen haben sollen. Nun, natürlich wurden einem dabei weitere Informationen gegeben, nämlich dass man von der Existenz einer Funktion ausgehen darf, die gleichverteilt zufällig eine reelle Zahl zwischen (jeweils inklusive) \(0\) und \(1\) liefert. Im Computer werden reelle Zahlen durch Doubles oder Floats dargestellt. Es gibt also nur endlich viele Zufallszahlen, die der PC liefern kann. Das waren dann aber auch schon alle Informationen. Je nachdem in welcher Programmiersprache man die Aufgabe lösen sollte, wurde einem dann noch die entsprechende Funktion, die Zufallszahlen liefert, genannt (in Java z. B. Math.random()). Die konkrete Frage- bzw. Aufgabenstellung lautet also: "Wie kann man mithilfe der Funktion Math.random() die Kreiszahl \(\pi\) berechnen bzw. möglichst gut schätzen?"
2. Vorüberlegungen
Wir sollen also nur die Funktion Math.random() als Lieferant für Pseudozufallszahlen verwenden, um \(\pi\) zu berechnen bzw. zu axpproximieren. Zuerst rufen wir uns in Erinnerung, was \(\pi\)
überhaupt ist. Die Kreiszahl \(\pi\) beschreibt das Verhältnis des Umfangs eines Kreises zu seinem Durchmesser. Um also \(\pi\) mit einer Zufallszahl schätzen zu können, benötigen wir irgendwie einen
Kreis.
Betrachten wir dazu einfach ein Koordinatensystem, in das ein Einheitskreis gezeichnet wird. Das ist ein Kreis mit dem Radius \(1\).
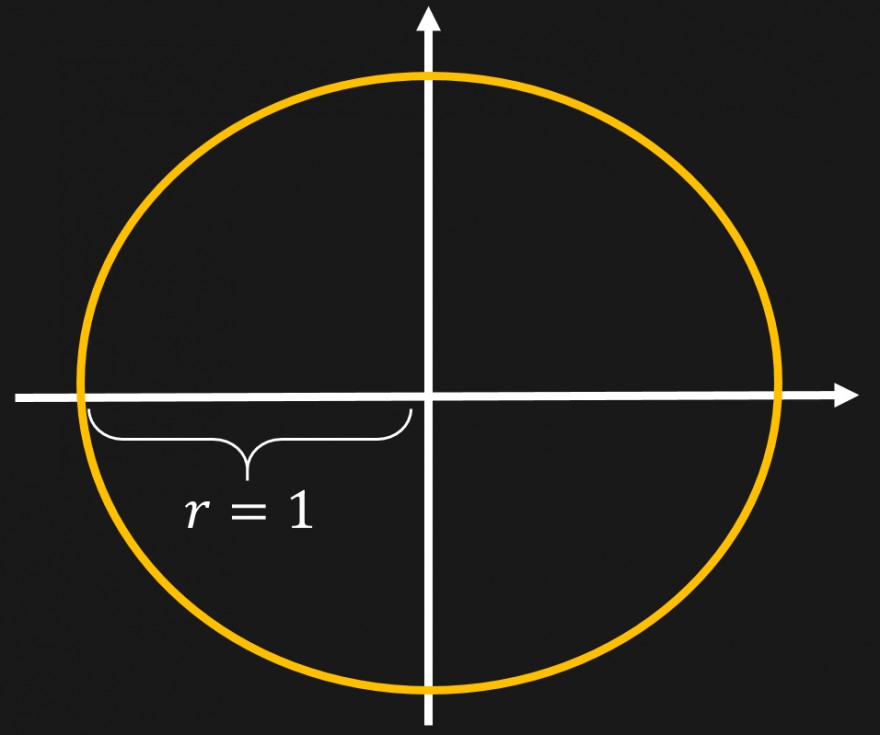
Dieser Kreis liegt innerhalb eines Quadrats, das die Seitenlängen \(2r\) (also den Durchmesser des Kreises) hat.
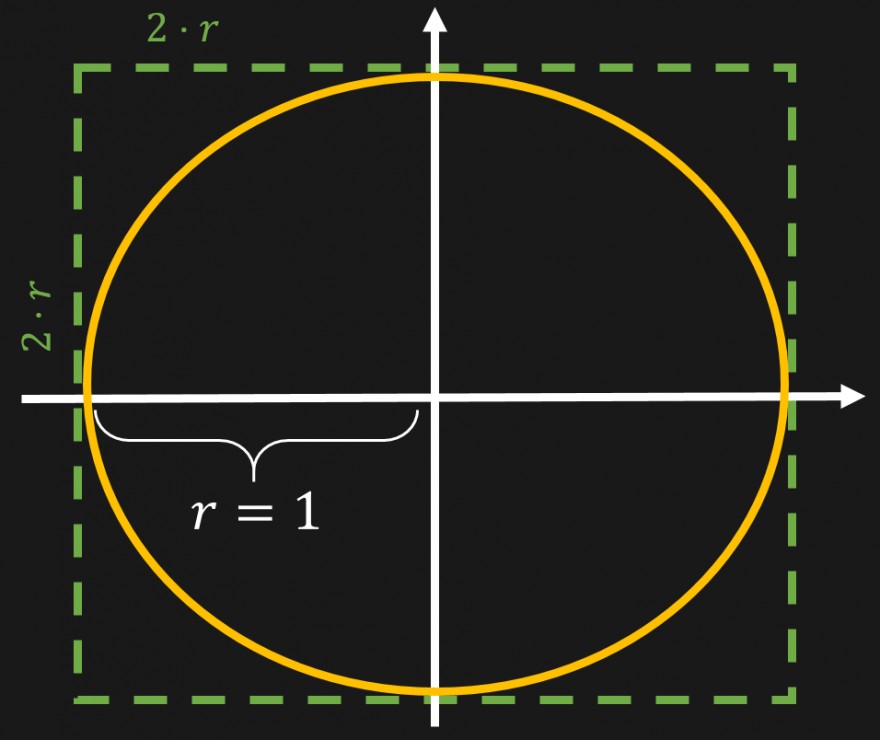
Da wir uns in einem Einheitskreis befinden, ist diese Seitenlänge \(2\cdot 1=2\), doch dazu später mehr.
Wenn wir die Random-Funktion zweimal hintereinander ausführen, dann erhalten wir dadurch einen Punkt, der irgendwo im rechten oberen Bereich des Koordinatensystems liegt. Das liegt daran, dass wir für jede der beiden Koordinaten nur Werte zwischen \(0\) und \(1\) erhalten.
Wir können für diese Punkte sogar aussagen, ob sie innerhalb oder außerhalb des Kreises liegen. Wenn nämlich der Abstand des Punktes zum Koordinatenursprung kleiner als \(1\) ist, dann liegt der Punkt innerhalb des Kreises, weil wir einen Einheitskreis gezeichnet haben. Wie berechnet man den Abstand zum Ursprung? Nun, mit dem Satz des Pythagoras kommt man schnell darauf, dass sich dieser Abstand mit der \(x-\) und \(y-\)Koordinate wie folgt berechnen lässt: $$ \sqrt{x^2+y^2} $$ Wir könnten theoretisch auch entscheiden, ob Punkte außerhalb des Kreises liegen, doch das ist an dieser Stelle gar nicht nötig. Warum nicht? Wir wollen innerhalb dieses Koordinatensystems einen geometrischen Zusammenhang finden, in dem \(\pi\) auftaucht und den wir dazu nutzen können, um mit den zufällig ermittelten Punkten und dem Wissen um den Einheitskreis \(\pi\) schätzen zu können.
Man kann das Verhältnis des Flächeninhalts des großen Kreises

und des großen Quadrats

auf das Verhältnis des Viertelkreises im rechten oberen Koordinatenabschnitt zu dem Quadrat im selben Quadranten runterechnen. D. h. also, wenn wir uns das Verhältnis der Flächeninhalte des großen Kreises zu dem des großen Quadrats ermitteln, dann entspricht das in etwa der dem Verhältnis der Anzahl an Punkten innerhalb des Kreisausschnitts zur Anzahl aller Punkte in dem entsprechenden Quadrat. Je mehr Punkte wir haben, desto exakter wird das Ergebnis!
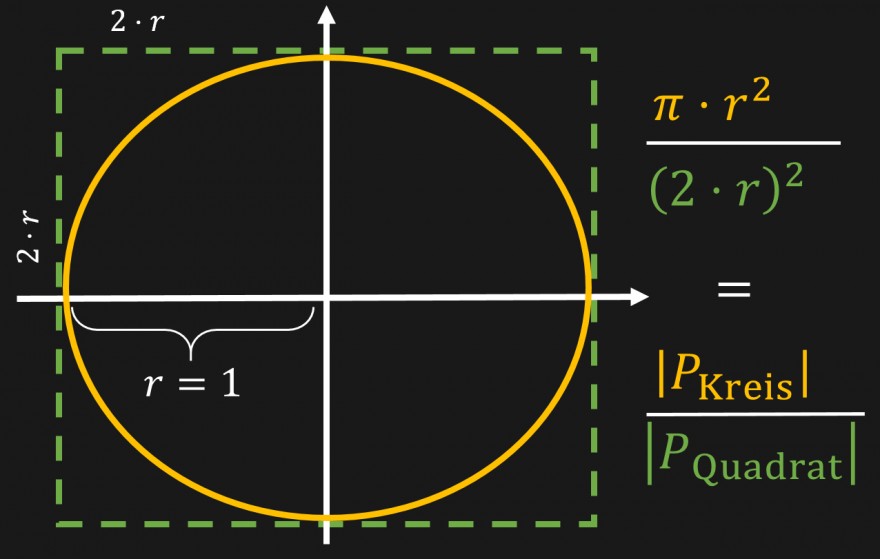
Mit dem Wissen, dass es sich um einen Einheitskreis handelt, ist \(r=1\). Dadurch wird die Gleichung zu: $$ \frac{\pi}{4}=\frac{\left|P_{\text{Kreis}}\right|}{\left|P_{\text{Quadrat}}\right|} $$ Wenn du beide Seiten der Gleichungen mit \(4\) multiplizierst, dann erhältst du als Ergebnis: $$ \pi=4\cdot \frac{\left|P_{\text{Kreis}}\right|}{\left|P_{\text{Quadrat}}\right|} $$ Du ermittelst also mit der Random-Funktion \(n\) Punkte, berechnest das Verhältnis der Punkte innerhalb des Kreises zu allen Punkten, die gemessen wurden und multiplizierst dieses Ergebnis mit \(4\). Je mehr Punkte du berechnest, desto genauer wird die Schätzung. Sie liefert übrigens für ein festes \(n\) nicht immer dasselbe Ergebnis, da die Punkte zufällig ermittelt werden.
Wir werden nun ein Java-Programm schreiben, mit dem wir unsere bisherige Theorie in die Praxis übertragen und experimentell überprüfen können, ob wir richtig liegen.
3. Java-Programm
Zuerst definieren wir eine Funktion mit dem Namen random_pi. Diese erhält als Übergabeparameter die Anzahl der zufälligen Punkte, die in die Berechnung eingehen sollen.
public static double random_pi(final int n){
return 0;
}
Nun benötigen wir zwei Variablen. Eine für die Anzahl der Punkte im Kreis und eine für die Anzahl der Punkte im Quadrat.
public static double random_pi(final int n){
int p_circle = 0;
int p_square = 0;
return 0;
}
In einer For-Schleife durchlaufen wir die Anzahl der zufälligen Punkte. Wir erzeugen in jedem Schleifendurchlauf einen Punkt mit einem zufälligen \(x-\) und \(y-\)Wert. Die Distanz eines Punktes zum Ursprung entscheidet, ob ein Punkt innerhalb oder außerhalb des Einheitskreises liegt. Die Distanz wird ermittelt, indem man die Wurzel aus der Summe des Quadrats der \(x-\) umd der \(y-\)Koordinate berechnet.
public static double random_pi(final int n){
int p_circle = 0;
int p_square = 0;
for(int i = 0; i < n; i++) {
double[] point = new double[] {Math.random(), Math.random()};
double distance = Math.sqrt(Math.pow(point[0], 2) + Math.pow(point[1], 2));
}
return 0;
}
Wenn der zuvor berechnete Abstand kleiner als \(1\) ist, dann wird die Anzahl der Punkte innerhalb des Kreises erhöht. Unabhängig von der Erhöhung der Anzahl an Punkten innerhalb des Kreises, wird die Anzahl der Punkte im Quadrat in jedem Schritt um \(1\) erhöht.
public static double random_pi(final int n){
int p_circle = 0;
int p_square = 0;
for(int i = 0; i < n; i++) {
double[] point = new double[] {Math.random(), Math.random()};
double distance = Math.sqrt(Math.pow(point[0], 2) + Math.pow(point[1], 2));
if(distance < 1){
p_circle++;
}
p_square++;
}
return 0;
}
Zum Schluss wird als Ergebnis das Vierfache des Verhältnisses der Punkte innerhalb und außerhalb des Kreises zurückgegeben. Das war der formale Zusammenhang, den wir uns zuvor hergeleitet haben.
Bereits ab \(1.000.000\) Punkten werden die ersten drei Nachkommastellen sehr zuverlässig korrekt angegeben.
Happy Pi-Day 2020! :)