1. Einführung
Wie entscheidet Goolge, ob eine Seite relevant oder nicht relevant ist? Warum sind bestimmte Seiten weiter oben in den Suchergebnissen zu finden, während andere irgendwo auf der 3. Seite ganz unten landen, wenn man z. B. nach dem Wort "Informatikstudium" sucht? Eine Antwort darauf liefert u. a. der Page Rank Algorithmus von Google. Er ist das bekannteste Verfahren zur Gewichtung bzw. Bewertung von Webseiten und wurde Ende der 1990er Jahre von Sergey Brin und Lawrence Page an der Stanford University entwickelt. Bei diesem Ansatz spielt die Verlinkungsstruktur der Webseiten untereinander eine wichtige Rolle.
2. Der Algorithmus
Wie läuft der Algorithmus ab?
Algorithmus: Google Page Rank
Eingabe: Netzwerk aus Webseiten, die ggf. aufeinander verlinken
Ausgabe: Rangfolge der Webseiten
1. Erstelle eine Matrix, mit der die Verlinkungen der Webseiten untereinander beschrieben werden.
2. Definiere einen Vektor, der so viele Zeilen hat wie die Matrix aus Schritt 1 Spalten besitzt. Trage dort für jeden Wert \(\frac{1}{\left|\text{Zeilen des Vektors}\right|}\) ein.
3. Multipliziere den Vektor aus Schritt 2 rechts an die Matrix aus Schritt 1.
4. Wiederhole Schritt 3 mit dem Vektor, der bei Schritt 3 als Ergebnis herauskommt.
5. Wiederhole Schritt 4 solange, bis sich keine Änderungen mehr im Ergebnisvektor ergeben.
Das ist bislang noch eine sehr theoretische Betrachtung. Wir werden den Algorithmus nun auf ein Mikro-Internet anwenden, das nur aus den Webseiten Facebook, YouTube, Amazon und Netflix bestehe.
3. Beispiel
Als Beispiel gehen wir von insgesamt 4 Webseiten, nämlich Facebook, YouTube, Amazon und NETFLIX aus. Diese Seiten verlinken aufeinander:
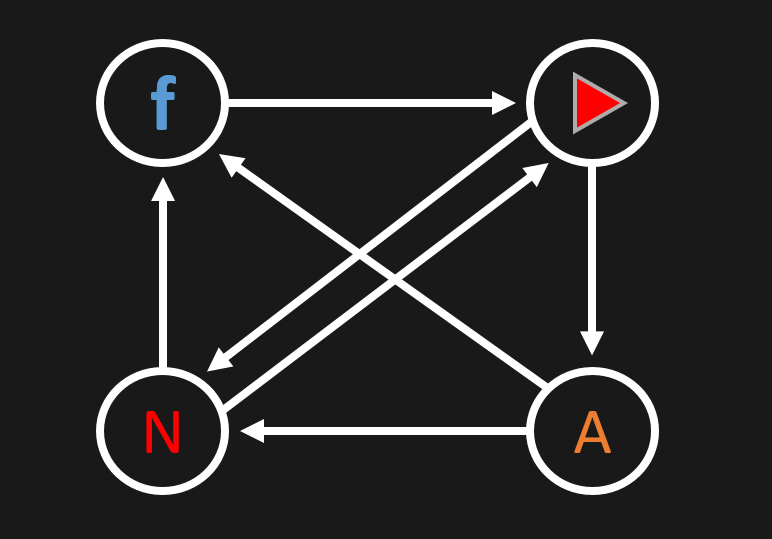
Wir nehmen an, dass jede Seite durch einen Link auf eine andere Seite einen Punkt (100%) vergeben kann. Der Punkt wird gleichmäßig aufgeteilt, wenn eine Seite auf mehr als eine andere Seite verlinkt. Amazon verweist z. B. auf Facebook und Netflix, d. h. von Amazon bekommen beide Webseiten jeweils einen halben Punkt. Facebook verweist z. B. nur auf YouTube, d. h. YouTube erhält einen ganzen Punkt.
Der erste Schritt des Algorithmus sieht vor, dass wir aus dem Netzwerk der Webseiten eine Matrix erzeugen. Wie machen wir das? Nun, wir schreiben an die Zeilen und Spalten die Webseiten und lesen dann die Verlinkungen mit den entsprechenden Gewichtungen (den Punkte) ab. Dabei gehen wir spaltenweise vor und ermitteln so für jede Seite, worauf sie verweist.
Facebook verweist nicht auf sich selbst, sondern nur auf YouTube, weshalb in der zweiten Zeile und der ersten Spalte eine 1 eingetragen wird.
- Von Facebook aus führt außerdem auch kein Link auf Amazon und Netflix.
- Von YouTube aus wird auf Amazon und Netflix verlinkt. Beide erhalten jeweils einen halben Punkt. Auf Facebook und sich selbst wird nicht verwiesen.
- Von Amazon wird auf Facebook verlinkt, nicht aber auf YouTube oder sich selbst. Zudem führt ein Link von Amazon direkt zu Netflix.
- Zu guter letzt wird von Netflix sowohl auf Facebook, als auch auf YouTube verwiesen (Netflix und YouTube referenzieren sich gegenseitig). Netflix verlinkt auf keine weitere Seite.
Als Ergebnis erhältst du die folgende Matrix: $$\left(\begin{matrix}0&0&0.5&0.5\\1&0&0&0.5\\0&0.5&0&0\\0&0.5&0.5&0\end{matrix}\right)$$ Beachte, dass die Summe der Einträge in den Spalten jeweils 1 ergibt. In den Einträgen entlang einer Zeile muss das nicht der Fall sein! Die Summe der Zeilen gibt auch nicht automatisch darüber Aufschluss, welche Seiten später wie geranked werden!
Die zuvor berechneten "Punkte", die entlang den Links für die einzelnen Webseiten vergeben werden, stellen Wahrscheinlichkeiten dar, die beim zufälligen Klicken auf einen Seitenlink zu einer (anderen) Seite führen. Da in dem Modell von einem "zufällig" klickenden User ausgegangen wird, werden die Punkte gleichmäßig auf die jeweiligen Verlinkungen aufgeteilt. Der Algorithmus soll nun ermitteln, auf welchen Seiten sich ein Benutzer, der eine sehr lange Zeit zufällig auf die Links im Netzwerk klickt, am wahrscheinlichsten aufhält.
Zu Beginn gehen wir davon aus, dass jede der vier Seiten mit derselben Wahrscheinlichkeit besucht werden kann. Wir verwenden als Vektor demnach $$ \left(\begin{matrix}0.25\\0.25\\0.25\\0.25\end{matrix}\right) $$ Wenn wir diesen Vektor rechts an unsere Gewichtungsmatrix multiplizieren, erhalten wir das folgende Ergebnis: $$ \left(\begin{matrix}0&0&0.5&0.5\\1&0&0&0.5\\0&0.5&0&0\\0&0.5&0.5&0\end{matrix}\right)\cdot\left(\begin{matrix}0.25\\0.25\\0.25\\0.25\end{matrix}\right) = \left(\begin{matrix}0.25\\0.375\\0.125\\0.25\end{matrix}\right) $$ Dieses Ergebnis gibt die Wahrscheinlichkeiten dafür an, auf welcher Seite man sich nach einem zufälligen Link-Klick befindet. Wie du siehst, werden Facebook und Netflix aktuell noch gleich geranked bzw. mit derselben Wahrscheinlichkeit durch einen zufälligen Link-Klick besucht. Das ändert sich aber bald!
Den PageRank Algorithmus interessiert, wo man sich nach seeehr vielen Link-Klicks mit welcher Wahrscheinlichkeit befindet. Deshalb führen wir mit dem Ergebnisvektor eine erneute Matrizenmultiplikation durch, um zu schauen, wo wir uns nach zwei zufälligen Link-Klicks mit welcherWahrscheinlichkeit auf welcher Seite befinden. $$ \left(\begin{matrix}0&0&0.5&0.5\\1&0&0&0.5\\0&0.5&0&0\\0&0.5&0.5&0\end{matrix}\right) \cdot\left(\begin{matrix}0.25\\0.375\\0.125\\0.25\end{matrix}\right) = \left(\begin{matrix}0.1875\\0.375\\0.1875\\0.25\end{matrix}\right) $$ Nach dem zweiten Klick ist auf einmal die Wahrscheinlichkeit, dass man auf Facebook oder Amazon landet gleich, während man mit einer höheren Wahrscheinlichkeit auf Netflix landet, obwohl nach dem ersten Klick die Wahrscheinlichkeit auf Facebook und Netflix zu landen gleich war. Das hat sich nun geändert!
Wie sieht es nach drei Klicks aus? Nun, du führst erneut die Matrizenmultiplikation mit dem zuvor berechneten Vektor durch und erhältst als Ergebnis $$ \left(\begin{matrix}0&0&0.5&0.5\\1&0&0&0.5\\0&0.5&0&0\\0&0.5&0.5&0\end{matrix}\right) \cdot\left(\begin{matrix}0.1875\\0.375\\0.1875\\0.25\end{matrix}\right) = \left(\begin{matrix}0.21875\\0.3125\\0.1875\\0.28125\end{matrix}\right) $$ Das ganze wiederholst du ein paar mal! Irgendwann stellst du fest, dass sich an den Werten irgendwann nichts mehr ändert und sie sich stabilisieren (in der Mathematik sagt man, dass sie gegen einen bestimmten Wert konvergieren), nämlich: $$ \left( \begin{matrix} 0.217391\\0.347826\\0.173913\\0.26087 \end{matrix} \right) $$ Du könntest auf dasselbe Ergebnis kommen, indem du einfach die \(n-\)te Potenz \(A^n\) der Matrix \(A\) berechnest und dieses Ergebnis dann mit dem Ausgangsvektor multiplizierst. Dabei lässt du \(n\) gegen unendlich laufen, da wir erfahren wollen, wie wahrscheinlich der Besuch auf bestimmten Webseiten ist, wenn ein Nutzer seehr lange wild umherklickt. $$ \lim\limits_{n\rightarrow\infty}\left(\begin{matrix}0&0&0.5&0.5\\1&0&0&0.5\\0&0.5&0&0\\0&0.5&0.5&0\end{matrix}\right)^n \cdot\left(\begin{matrix}0.25\\0.25\\0.25\\0.25\end{matrix}\right) = \left(\begin{matrix}0.21875\\0.3125\\0.1875\\0.28125\end{matrix}\right) $$ Das, was du dort als Ergebnis herausbekommst ist übrigens ein Eigenvektor der Matrix! Mit diesem Verfahren wird nämlich im Prinzip eine Markov-Kette beschrieben, die man aus der Schule und dem Studium oft nur für Berechnung von Mäusepopulationen oder ähnlichen alltagsfernen Zusammenhängen nutzt. Wir haben nämlich ein System mit konstanten Wahrscheinlichkeiten und wechseln zwischen endlich vielen Zuständen (den einzelnen Webseiten) hin und her. Zudem besitzt unsere Matrix zur Darstellung der Verlinkungen der Webseiten untereinander die wichtige Eigenschaft einer Übergangsmatrix im Markov-Prozess, nämlich dass ihre Spalten in Summe den Wert \(1\) besitzen. Jetzt hast du mal ein Beispiel kennengelernt, das auch dich im alltäglichen Leben betrifft.
Interessant ist an diesem Ergebnis übrigens auch, dass Netflix in unserem Beispiel höher geranked wird als Facebook, obwohl auf beide Seiten zwei Links verweisen. Das liegt u. a. daran, dass YouTube auf Netflix verweist und YouTube einen sehr hohen Rang besitzt. Übertragen wir diese Überlegung in die reale Welt, dann wird vielleicht klarer, weshalb Seiten, die von großen Seiten wie YouTube, Spiegel, FAZ oder web-de verlinkt werden, weiter vorne im Google-Ranking zu finden sind als andere.
In der Realität wird der Algorithmus nicht nur auf ein Netzwerk von vier, sondern auf alle Seiten im Internet angewendet. Natürlich bedarf es hierfür einer Reihe von Optimierungen, da Matrizenmultiplikationen im Aufwand quadratisch ansteigen und das ab einer bestimmten Anzahl an Webseiten auch nicht mehr mit massiver Rechenpower gelöst werden kann. Deshalb ist die Theorie aus der linearen Algebra wichtig. Insbesondere Eigenwerte und Eigenvektoren spielen dabei eine Rolle. Auch die Art und Weise, wie Matrizen im Computer im gespeichert, ist dabei relevant.
Der Algorithmus für die heutige Berechnung der Relevanz von Seiten und ihr Ranking im Internet wurde von Goolge im Laufe der Zeit angepasst und erweitert. Im Kern fußt die Idee aber noch auf den vor etwa 20 Jahren initial entwickelten PageRank Algorithmus.
Autor: Florian André Dalwigk
Dieser Artikel hat 50 Bonuspunkte erhalten. Schreib auch du einen Artikel.