Ich gehe in diesem Artikel nicht auf die Grundlagen ein, sondern möchte zeigen, wie mit einer Tabellenkalkulation (z.B. Google-Tab) ein Simplex-Programm "elegant" durchgerechnet werden kann.
In Spalte A stehen die Zielfunktion Z(x1,x2) und die einzuhaltenden Nebenbedingungen als Ungleichungen. Ganz ungeduldige können das Programm von Maxima-Online↥ durchrechnen lassen:
load(simplex);
maximize_lp(
6*x+4*y,[
5*x+4*y<=1000,
7*x+3*y<=800,
1*x<=100,
y<=160
]
), nonegative_lp=true;
Das Start-Tableau ist durch die Spalten x1 x2 und die Basis-Spalten s1 s2 s3 s4 (Schlupfvariablen) so wie die b-Spalte (die rechten Seiten der zu Gleichungen umgebauten Nebenbedingungen) definiert.
1. Suche Pivotspalte [Min(G)] Minimum Zeile G ↦Pivotspalte = 1
2.Teile b-Spalte durch positive Werte der Pivotspalte:
Formel nach bis Zeile s3 kopieren (lösche ggf. b=DIV#0 oder b<0 )
Zeile s3 kleinster Wert>0 ↦PivotZeile = 3
3. Pivotzeile in neues Tableau übernehmen und durch Pivotelement dividieren. Die neuen Pivotzeile hat eine 1 in der Pivotspalte. Zu allen übrigen Zeilen addieren, dass in Pivotspalte eine Null entsteht.
4. Neues Tableau erstellt: Gehe zu 1.
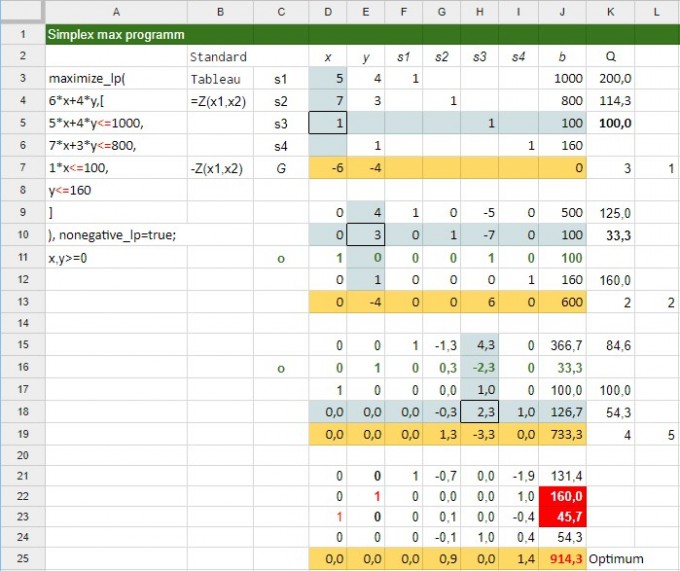
Hier noch ein Link auf die Google-Tabelle Simplex-Algorithmus↥ ...
YouTube↥: Arbeitsschritte vom Start-Tableau zum optimalen Tableau