Primales Problem mit dem dualen Simplex Algorithmus lösen

Question

Lösen Sie das folgende Problem sowohl mit dem erweiterten Simplex-Algorithmus als auch mit dem dualen Simplex-Algorithmus.

$$( P ) \left\{ \begin{aligned} 2 x _ { 1 } + 3 x _ { 2 } + 4 x _ { 3 } & \rightarrow \min \\ x _ { 1 } + 2 x _ { 2 } + x _ { 3 } & \geq 3 \\ 2 x _ { 1 } - x _ { 2 } + 3 x _ { 3 } & \geq 4 \\ x _ { 1 } , x _ { 2 } , x _ { 3 } & \geq 0 \end{aligned} \right.$$

Ich habe zuerst das Problem mit dem primalen Simplex- Algorithmus gelöst und erhielt als Basislösung (11/5,2/5,0,0,0), als Ecklösung (11/5,2/5).

Nun solle ich das Problem mit dem dualen Simplex Algorithmus lösen. Ich dachte ich müsste das Problem zuerst in ein duales Problem anfangen und damit dann den dualen Simplex Algorithmus anwenden. In den Lösung fangen diese direkt mit den dualen Simplex Algorithmus an und wandeln, das Problem nicht um, aber wieso`?

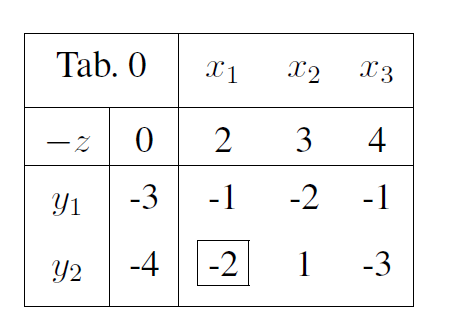
Wieso muss ich das Problem nicht zuerst in ein duales Problem umwandeln, sondern kann direkt anfangen?

Ich würde mich sehr über eine Antwort freuen.

Answer 1

Du gehst zum wiederholten Male davon aus, dass die von euch angewendeten Algorithmen und Tableauschreibweisen allgemein bekannt sind - sind sie nicht.

Suche nach Autoren, die euere Verfahrensweisen anwenden und erklären oder bereite Deine Frage so auf, dass entsprechende Hintergrund-Informationen zur Verfügung stehen ...

Inhaltlich zu Deiner Frage: In meiner Simplexwelt ist der Algorithmus immer der gleiche - es gibt keinen speziellen Algorithmus-duales-Programm. Zu Beginn steht die Transponierung der Gleichungsmatrix, das Ausrichten der NB und dann geht es seinen Gang - wie im Standard-Programm auch.

Z.B.