Aufgabe:
Meine Aufgaben: Ich sollte zunächst einmal einen Simplex Algorithmus aufstellen und lösen (Bild 1).
Danach sollte ich das Problem von Primal nach Dual umwandeln (Bild 2).
Anschließend sollte ich diesen Simplex ebenfalls lösen (Bild 3).
Bis hier habe ich alles geschafft, auch weil es erlaubt war ein Programm zu nutzen um diese Algorithmen zu lösen.
Nun soll ich die Lösung vom Dualen Simplex Algrithmus wirtschaftlich interpretieren (Schattenpreise etc.), hier von habe ich überhaupt gar keine Lösung, wisst ihr da bescheid?
1.
Text erkannt:
\begin{tabular}{|c|c|c|c|c|c|c|c|}
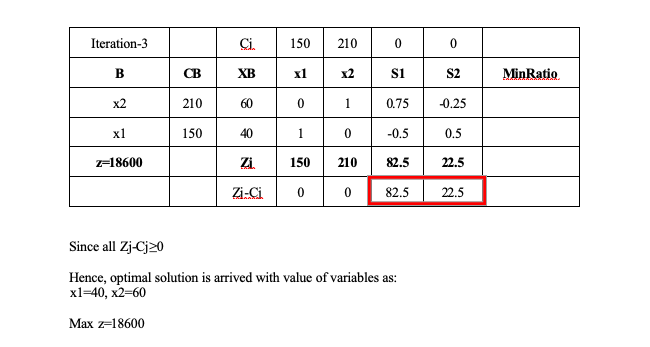
\hline Iteration-3 & & Ci & 150 & 210 & 0 & 0 & \\
\hline B & CB & XB & x1 & x2 & S1 & S2 & MinRatia \\
\hline x2 & 210 & 60 & 0 & 1 & 0.75 & 0.25 & \\
\hline x1 & 150 & 40 & 1 & 0 & -0.5 & 0.5 & \\
\hline z=18600 & & Zi. & \( \mathbf{1 5 0} \) & \( \mathbf{2 1 0} \) & 82.5 & 22.5 & \\
\hline & & Zi-Ci & 0 & 0 & 82.5 & 22.5 & \\
\hline
\end{tabular}
since all Zj-Cj\geq0
Hence, optimal solution is arrived with value of variables as:
\( x 1=40, x 2=60 \)
Max \( z=18600 \)
2.
Text erkannt:
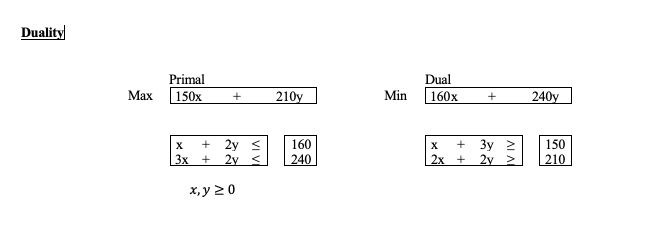
Duality
\begin{tabular}{|lcc|}
\hline Primal & & \\
\hline \( 150 \mathrm{x} \) & \( + \) & \( 210 \mathrm{y} \) \\
\hline
\end{tabular} \( \operatorname{Max}|150 \mathrm{x}+210 \mathrm{y}| \quad \) Min
\begin{tabular}{l}
Dual \\
\hline \( 160 x+1 \)
\end{tabular} \( 240 y \)
\begin{tabular}{|lccc|c|}
\hline \( \mathrm{x} \) & \( + \) & \( 2 \mathrm{y} \) & \( \leq \) \\
\( 3 \mathrm{x} \) & \( + \) & \( 2 \mathrm{y} \) & \( \leq \) \\
\hline
\end{tabular} \begin{tabular}{|lccc|c|}
\hline \( \mathrm{x} \) & \( + \) & \( 3 \mathrm{y} \) & \( \geq \) & 150 \\
\( 2 \mathrm{x} \) & \( + \) & \( 2 \mathrm{y} \) & \( \geq \) & 210 \\
\hline
\end{tabular}
$$ x, y \geq 0 $$
3.
Text erkannt:
\begin{tabular}{|c|c|c|c|c|c|c|c|}
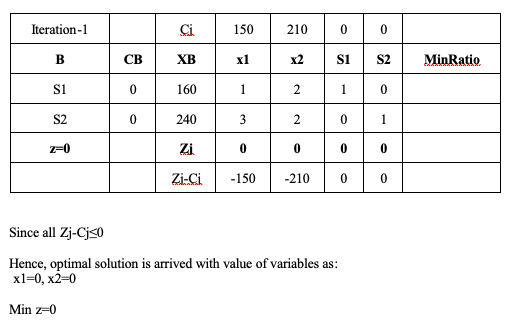
\hline Iteration-1 & & Ci & 150 & 210 & 0 & 0 & \\
\hline B & CB & XB & x1 & x2 & S1 & S2 & MinRatio \\
\hline S1 & 0 & 160 & 1 & 2 & 1 & 0 & \\
\hline S2 & 0 & 240 & 3 & 2 & 0 & 1 & \\
\hline z=0 & & Zi & 0 & 0 & 0 & 0 & \\
\hline & & Zi-Ci & -150 & -210 & 0 & 0 & \\
\hline
\end{tabular}
since all \( Z j-C j \leq 0 \)
Hence, optimal solution is arrived with value of variables as:
\( x 1=0, x 2=0 \)
Min \( z=0 \)