An welcher Stelle schneidet die Tangente die x-Achse?

Question

Haallooo :)

Ich war jetzt eine Woche wegen ner Grippe nicht in der Schule und komm in Mathe irgendwie nicht mehr mit... Also Thema sind "Ableitungen" und die Aufgabe lautet:


P ist ein Punkt des Graphen von f. Bestimme die Gleichung der Tangente t durch den Punkt P.

An welcher Stelle schneidet die Tangente die x-Achse?

f mit f(x) = -x² ; P (2/ f (2))


Wäre super wenn ihr mir helfen könntet schreib nämlich nächste Woche eine Klausur zu dem Thema...

Answer 1

hi

f(x) = -x²
P = (x1 | y1) = (2|f(2)) = (2|-4)

erste ableitung von f(x) berechnen
f'(x) = -2x
die steigung der tangente an der stelle x = 2 ist
f'(2) = -2*2 = -4

ansatz für tangentengleichung mit punkt-steigungsform
f'(x) = (y-y1)/(x-x1)
f'(x)(x-x1) = y-y1
y = f'(x)(x - x1) + y1
das ist die gleichung einer tangente

für die gleichung durch den punkt P(2|-4) setzen wir die
koordinaten x1 = 2 und y2 = -4 sowie die steigunt f'(2) = -4 ein.
y = t(x) = -4(x - 2) - 4
y = t(x) = -4x + 4
das ist die geradengleichung der tangente, die durch den punkt
P(2|-4) geht.
 

Answer 2

 

wie man eine Funktion ableitet, weißt Du? Man multipliziert die Variable mit dem Exponenten und subtrahiert dann vom Exponenten 1, also

f(x) = -x²

f'(x) = -2 * x^2-1 = -2x

Der Punkt P(2|f(2)) = P(2|-2²) = P(2|-4) hat also dann den Anstieg

f'(2) = -2 * 2 = -4

 

Diesen Anstieg muss auch die Tangente im besagten Punkt haben.

Tangentengleichung allgemein:

y = mx + b, wobei m die Steigung ist und b der y-Achsenabschnitt.

Besser schreibt man die Tangentengleichung bei einer Aufgabe wie dieser

t(x) = f'(x₀) * (x - x₀) + f(x₀)

x₀ ist die Stelle, die uns interessiert, also x = 2

f'(2) = -4 wie oben berechnet

f(2) = -4 wie oben berechnet

Also lautet die Tangentengleichung

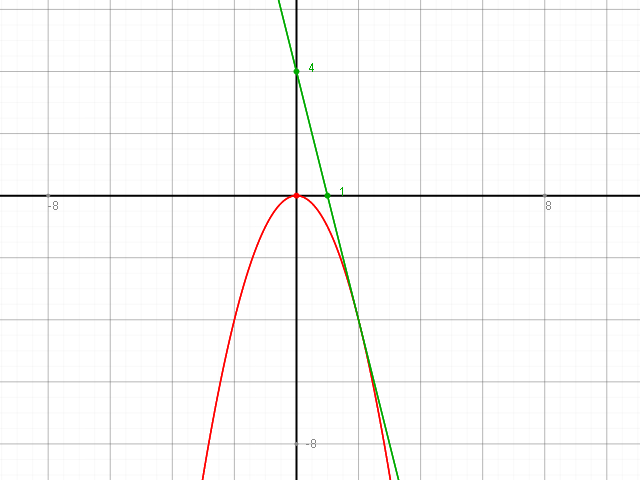
t(x) = -4 * (x - 2) - 4 = -4x + 8 - 4 = -4x + 4

 

Wo schneidet diese Tangente die x-Achse? y = 0 setzen:

0 = -4x + 4

x = 1

 

 

Besten Gruß