Aus nachstehender Skizze folgt, dass diese Formel nicht stimmen kann.
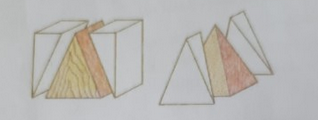
In der Tat gilt für das Volumen einer Pyramide folgende Formel:
$$ V=\frac{1}{3} \cdot G \cdot h $$
Einen Beweis für diese Formel werden wir später erbringen, zunächst können wir folgenden Aufgaben erproben:
Aufgaben zur Pyramide:
1. Argumentiere in einigen Worten, warum mit obiger Skizze folgt, dass die Volumenformel die Pyramide nicht \( V=\frac{1}{2} \cdot G \cdot h \) sein kann!
2. Die Cheops-Pyramide in Ägypten hat angenähert die Form einer regulären vierseitigen Pyramide mit einer Höhe von \( 137 \mathrm{m} \) und einer Grundkante von \( 227 \mathrm{m} \). Berechne das Volumen und den Inhalt einer Seitenfläche.
3. Berechne den Dachraum (Volumen des Dachstockes) wie auch die Oberfläche des (gefärbte Fläche)
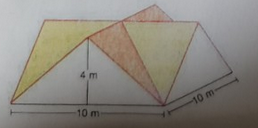
Aufgabe:
Ich habe Aufgabe 1-3 gelöst, bin mir aber nicht sicher mit meinem Ansatz. Wäre über eine Kontrolllösung von jemandem von euch dankbar.
Bei der Nr. 1 habe ich geschrieben: Weil die Pyramide oben auf der Skizze aus 3 Teilen besteht. Deshalb 1/3. Wie würdet ihr es formulieren?