Durchschnittsgeschwindigkeit-Zeit-Diagramm

Question

liebe Lounge,

angenommen, man hat ein Diagramm, welches die DURCHSCHNITTSgeschwindigkeit, also den aktuellen Kilometerstand zu einem Zeitpunkt x angibt (x ist die seit Beginn der Aufzeichnung verbrauchte Zeit) angibt.

Welche Bedeutung hätte dann das Integral?

Kann ja nicht auch der absolvierte Weg sein oder? Das hat man ja bereits, wenn man die momentangeschwindigkeit über die Zeit integriert...

Vielen Dank!!!

Comments

die DURCHSCHNITTSgeschwindigkeit, also den aktuellen Kilometerstand zu einem Zeitpunkt x angibt

Was hat das eine mit dem anderen zu tun?

Wie sieht das Diagramm genau aus? Wie sind die Achsen beschriftet?

Answer 1

Zu einen Zeitpunkt gibt es keine Durchschnittsgeschwindigkeit, sondern nur eine Momentangeschwindigkeit.

Meinst du vielleicht die Durchschnittsgeschwindigkeit vom Start BIS zum aktuellen Zeitpunkt?

Comments

Jap. Dachte, das hätte ich so geschrieben...

Answer 2

Momentangeschwindigkeit v ( t ) wird auf einem
Tacho angezeigt.

Der Weg ist das integral von v ( t ) dt zwischen
ta und te ( anfangszeit und endzeit )

Weg durch ( te - ta ) ist die Durchschnittsgeschwindigkeit.

Comments

Meine Uhr zeigt mir aber ebendies an.

Durchschnittsgeschwindigkeit für gefahrene Zeit x (vom Start an )

---

Enthält deine Uhr auch ein Geschwindigkeits-
messgerät ? Auf welcher Basis ?

---

Es gibt Uhren die ein GPS Modul enthalten.

Zusätzlich werden vorhandene Beschleunigungssensoren genutzt um die Genauigkeit zu verbessern oder um eventuell eine GPS Empfangslücke zu überbrücken.

---

Die Uhr gibt NUR die „aktuelle“ also bis zum jetzigen Zeitpunkt x generierte Durchschnittsgeschwindigkeit an.

Also gibt das Integral eigentlich keinen Sinn?

---

Der zum Zeitpunkt t momentane Wert der Geschwindigkeit werde durch den roten Graphen dargestellt, dann ergibt sich für den Wert der bis zum Zeitpunkt t erreichten Durchschnittsgeschwindigkeit der blaue Graph.

Text erkannt:

1

Aus beiden lässt sich der zurückgelegte Weg (grün) rekonstruieren, nämlich einmal als Fläche unter der Kurve (rot), bzw. einmal als Fläche des Rechtecks (blau).

Eine Integration der Durchschnitts-Geschwindigkeit ist dafür nicht nötig.

---

Ok. Aber die Frage nach der Bedeutung des Integrals wäre ja damit noch nicht geklärt...

---

Hallo Kombi,

ich verstehe nicht wo es bei dir hakelt. Ausgehend vom Geschwindigkeits / Zeit Diagramm ergibt sich

s = ∫ v ( t ) dt zwschen t(ende) minus t(anfang)

ist der Weg.

v ( mittel ) = Weg / [ t(ende) minus t(anfang) ]
ist Durchschnitts - v

Frag trotzdem weiter nach bis alles
klar ist.
Die Zusammenhänge sind elementar und
kommen immer wieder vor.

---

Also, nochmal genauer zu dem, um was es mir geht.

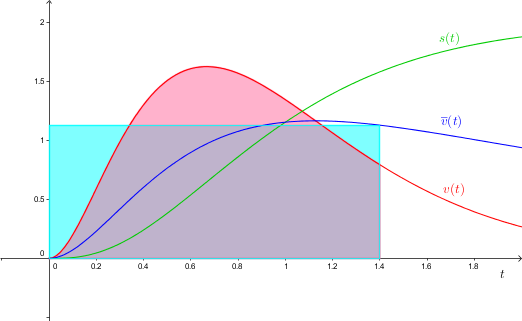
Betrachten wir v_blau als eine Funktion, welche einem Zeitpunkt x die bis dahin zugehörige Durchschnittsgeschwindigkeit zuordnet.

Also im Prinzip:  v_blau= 1/x  \( \int\limits_{0}^{x} \)v(t) dt oder nicht?

Aus beiden lässt sich der zurückgelegte Weg (grün) rekonstruieren, nämlich einmal als Fläche unter der Kurve (rot), bzw. einmal als Fläche des Rechtecks (blau).

In dieser Aussage steckt meine Frage implizit drin. Der Flächeninhalt des Rechtecks mit der Höhe v_blau(x) und der Breite x gibt die in der Zeit 0 - x zurückgelegte Strecke an.

Offensichtlich ist der Wert dieser Fläche ein anderer, als wenn man das bestimmte Integral von der Funktion  v_blau bestimmt, also

\( \int\limits_{0}^{x} \) v_blau(t) dt, mit x ist ein beliebiger aber fester Zeitpunkt.

---

Gehen wir einmal von der Momentan-
geschwindigkeit aus
Diese liegt als Funktion von t vor.
Angenommen
v ( t ) = 1/2 * t^2

v ( 0 ) = 0
Stammfunktion
1/2 * t^3 / 3
Integrationsanfang x = 0
Weg ist auch  ( x : beliebiger zeitpunkt )
s ( x ) = 1/2 * x^3 / 3

Die Durchschnittgeschwindigkeit ist
s / x = ( 1/2 * x^3 / 3 ) / x = x^2 / 6
man kann auch x = t nehmen
x^2 / 6

Hier der Graph für
Momentangeschwiindigkeit ( blau ) und
Durchschnittsgeschwindigkeit ( rot )

Was sind deine weiteren Fragen ?

---

Wie lässt sich das Integral deiner roten Funktion interpretieren?

Das ist eigentlich von Anfang an meine Frage gewesen :)! Weil es kann ja nicht der zurückgelegte Weg sein, da das ja schon das Integral der blauen Funktion ist. Und die beiden sind ja nicht identisch..

---

x^2 / 6
integralfunktion
( x^3/3 ) / 6
x^3 / 18

Dies ist nichs Bekanntes.
Ich wüßte nicht wozu man die Fläche
unterhalb der roten Kurve gebrauchen
könnte.

---

Wobei mich das immer noch beschäftigt...

Die Einheit auf der y Achse der Funktion der Durchschnittsgeschwindigkeit  bis zu einem Zeitpunkt t ist doch km/h (oder m/s, wie auch immer).

Die Einheit des Integrals ist ja die Einheit der x-Achse multipliziert mit der Einheit der y-Achse.

Demnach hat das Integral hier ebenfalls die Einheit km oder m, also eigentlich auch ein Weg...

Was kannst du mir dazu sagen !?

---

also eigentlich auch ein Weg...

Richtig. Und wenn du diesen Weg durch die verstrichene Zeit dividierst, dann erhätst du die mittlere Ducrchschnittsgeschwindigkeit